The "Gradient Flow"

This work is focused on the design of robust, efficient, and practical numerical schemes for bistable gradient equations (BGEs), which are (possibly highly nonlinear) PDEs that describe important phenomena in materials, fluids, and biology problems. In particular, epitaxial thin film growth (with or without slope selection), phase field crystal (PFC) and Cahn-Hilliard-Flow (CHF) type equations are studied in detail. These are important 4th or 6th-order BGEs that must typically be solved over large space and time scales. Numerical solution of these equations (and BGEs in general) can pose enormous challenges.
In my work, convex splitting (CS) schemes for BGEs are taken into consideration. The CS schemes are 1st or 2nd-order accurate in time and at least 2nd-order accurate in space. They are simple, powerful, and particularly well-suited to studying large spatiotemporal morphological evolution accurately and efficiently. 1st-order (in time) CS schemes have been known for about ten years; but, up to now, the underlying theory has been incomplete and their application, somewhat limited. The high-order CS schemes (2nd-order in time, 2nd-order and higher in space) are, I believe, novel features of this work.

All CS schemes have two important properties: they are unconditionally energy stable and unconditionally uniquely solvable. The energy stability can often be exploited to prove various norm stabilities, as well as convergence. The unique solvability follows from the fact that the schemes are derived as the gradients of strictly convex functionals. As a result, practical solvers can always be crafted, since gradient descent methods will converge unconditionally.

A big challenge of this work is in designing truly efficient solvers for the potentially highly nonlinear CS schemes. Some early, important successes in this direction are reported in my works, and nearly optimally efficient nonlinear multigrid solvers have been crafted for the PFC and Cahn-Hilliard-Hele-Shaw (CHHS) equations.

BGEs model a great number of physical and biological phenomena, and hence this work will have a direct and immediate impact on many scientific disciplines. These specific equations (thin film growth, PFC, and CHF type equations) are vital for understanding phase transformations of materials at the atomic and nanometer scales, the complex processes in biological growth and development, and the complicated topological change involved in two-phase flows. The efficient nonlinear and spatiotemporally adaptive solvers will apply to even more general equations than BGEs and will therefore advance the field of numerical nonlinear PDEs.

Additionally, the adaptive-multigrid software BSAM will be made available in the public domain so that researchers will have direct access to some of the algorithms developed.

1. An energy stable and convergent finite-difference scheme for the phase field crystal equation. S. Wise, C. Wang, J. Lowengrub, SIAM Journal on Numerical Analysis, 47, (2009), 2269-2288. PDF file
2. Stable and efficient finite-difference nonlinear-multigrid schemes for the phase field crystal equation. Z. Hu, S. Wise, C. Wang, J. Lowengrub, Journal of Computational Physics, 228, (2009), 5323-5339. PDF file
3. Unconditionally stable schemes for equations of thin film epitaxy. C. Wang, X. Wang, S. Wise, Discrete and Continuous Dynamical Systems-Series A, 28, (2010), 405-423. PDF file
4. Global smooth solutions of the three-dimensional modified phase field crystal equation. C. Wang, S. Wise, Methods and Applications of Analysis, 17, (2010), 191-212. PDF file
5. An energy stable and convergent finite-difference scheme for the modified phase field crystal equation. C. Wang, S. Wise, SIAM Journal on Numerical Analysis, 49, (2011), 945-969. PDF file
6. Second-order convex splitting schemes for gradient flows with Ehrlich-Schwoebel type energy: Application to thin film epitaxy. J. Shen, C. Wang, X. Wang, S. Wise, SIAM Journal on Numerical Analysis, 50, (2012), 105-125. PDF file
7. A linear energy stable scheme for a thin film model without slope selection. W. Chen, S. Conde, C. Wang, X. Wang, S. Wise, Journal of Scientific Computing, 52, (2012), 546-562. PDF file
8. Energy stable and efficient finite-difference nonlinear multigrid schemes for the modified phase field crystal equation. A. Baskaran, Z. Hu, J. Lowengrub, C. Wang, S. Wise, P. Zhou, Journal of Computational Physics, 250, (2013), 270-292. PDF file
9. Convergence analysis of a second order convex splitting scheme for the modified phase field crystal equation. A. Baskaran, J. Lowengrub, C. Wang, S. Wise, SIAM Journal on Numerical Analysis, 51, (2013), 2851-2873. PDF file
10. A linear iteration algorithm for a second order energy stable scheme for a thin film model without slope selection. W. Chen, C. Wang, X. Wang, S. Wise, Journal of Scientific Computing, 59, (2014), 574-601. PDF file
11. Second order convex splitting schemes for periodic nonlocal Cahn-Hilliard and Allen-Cahn equations. Z. Guan, J. Lowengrub, C. Wang, S. Wise, Journal of Computational Physics, 277, (2014), 48-71. PDF file
12. A convergent convex splitting scheme for the periodic nonlocal Cahn-Hilliard equation. Z. Guan, C. Wang, S. Wise, Numerische Mathematik, 128, (2014), 377-406. PDF file
13. An energy-conserving second order numerical scheme for nonlinear hyperbolic equation with an exponential nonlinear term. L. Wang, W. Chen, C. Wang, Journal of Computational and Applied Mathematics, 280, (2015), 347-366. PDF file
14. An $H^2$ convergence of a second-order convex-splitting, finite difference scheme for the three-dimensional Cahn-Hilliard equation. J. Guo, C. Wang, S. Wise, X. Yue, Communications in Mathematical Sciences, 14 (2016), 489-515. PDF file
15. Convergence analysis of a fully discrete finite difference scheme for Cahn-Hilliard-Hele-Shaw equation. W. Chen, Y. Liu, C. Wang, S. Wise, Mathematics of Computation, 85 (2016), 2231-2257. PDF file
16. Global-in-time Gevrey regularity solution for a class of bistable gradient flows. N. Chen, C. Wang, S. Wise, Discrete and Continuous Dynamical Systems-Series B, 21 (2016), 1689-1711. PDF file
17. An energy stable, hexagonal finite difference scheme for the 2D phase field crystal amplitude equations. Z. Guan, V. Heinonen, J. Lowengrub, C. Wang, S. Wise, Journal of Computational Physics, 321 (2016), 1026-1054. PDF file
18. Stability and convergence of a second order mixed finite element method for the Cahn-Hilliard equation. A. Diegel, C. Wang, S. Wise, IMA Journal of Numerical Analysis, 36 (2016), 1867-1897. PDF file
19. A second-order, weakly energy-stable pseudo-spectral scheme for the Cahn-Hilliard equation and its solution by the homogeneous linear iteration method. K. Cheng, C. Wang, S. Wise, X. Yue, Journal of Scientific Computing, Journal of Scientific Computing, 69 (2016), 1083-1114. PDF file
20. Preconditioned steepest descent methods for some regularized p-Laplacian problems. W. Feng, A. Salgado, C. Wang, S. Wise, Journal of Computational Physics, 334 (2017), 45-67. PDF file
21. Error analysis of a mixed finite element method for a Cahn-Hilliard-Hele-Shaw system. Y. Liu, W. Chen, C. Wang, S. Wise, Numerische Mathematik, 135 (2017), 679-709. PDF file
22. Error analysis of an energy stable finite difference scheme for the epitaxial thin film growth model with slope selection with an improved convergence constant. Z. Qiao, C. Wang, S. Wise, Z. Zhang, International Journal of Numerical Analysis and Modeling, 14 (2017), 283-305. PDF file
23. Convergence analysis and error estimates for a second order accurate finite element method for the Cahn-Hilliard-Navier-Stokes system. A. Diegel, C. Wang, X. Wang, S. Wise, Numerische Mathematik, 135 (2017), 495-534. PDF file
24. A second-order energy stable BDF numerical scheme for the Cahn-Hilliard equation. Y. Yan, W. Chen, C. Wang, S. Wise, Communications in Computational Physics, 23 (2018), 572-602. PDF file
25. Convergence analysis for second order accurate convex splitting scheme for the periodic nonlocal Allen-Cahn and Cahn-Hilliard equations. Z. Guan, J. Lowengrub, C. Wang, Mathematical Methods in the Applied Sciences, 40 (2017), 6836-6863. PDF file
26. Convergence analysis and numerical implementation of a second order numerical scheme for the three-dimensional phase field crystal equation. L. Dong, W. Feng, C. Wang, S. Wise, Z. Zhang, Computers & Mathematics with Applications, 75 (2018), 1912-1928. PDF file
27. Efficient energy stable schemes for isotropic and strongly anisotropic Cahn-Hilliard systems with the Willmore regularization. Y. Chen, J. Lowengrub, J. Shen, C. Wang, S. Wise, Journal of Computational Physics, 365 (2018), 56-73. PDF file
28. A second order energy stable linear scheme for a thin film model without slope selection. W. Li, W. Chen, C. Wang, Y. Yan, R, He, Journal of Scientific Computing, 76 (2018), 1905-1937. PDF file
29. A uniquely solvable, energy stable numerical scheme for the functionalized Cahn-Hilliard equation and its convergence analysis. W. Feng, Z. Guan, J. Lowengrub, C. Wang, S. Wise, Y. Chen, Journal of Scientific Computing, 76 (2018), 1938-1967. PDF file
30. A second-order energy stable Backward Differentiation Formula method for the epitaxial thin film equation with slope selection. W. Feng, C. Wang, S. Wise, Z. Zhang, Numerical Methods for Partial Differential Equations, 34 (2018), 1975-2007. PDF file
31. A second order energy stable scheme for the Cahn-Hilliard-Hele-Shaw equation. W. Chen, W. Feng, Y. Liu, C. Wang, S. Wise, Discrete and Continuous Dynamical Systems-Series B, 24 (2019), 149-182. PDF file
32. Optimal rate convergence analysis of a second order numerical scheme for the Poisson-Nernst-Planck system. J. Ding, C. Wang, S. Zhou, Numerical Mathematics: Theory, Methods and Applications, 12, (2019), 607-626. PDF file
33. An energy stable fourth order finite difference scheme for the Cahn-Hilliard equation. K. Cheng, W. Feng, C. Wang, S. Wise, Journal of Computational and Applied Mathematics, 362, (2019), 574-595. PDF file
34. An energy stable Fourier pseudo-spectral numerical scheme for the square phase field crystal equation. K. Cheng, C. Wang, S. Wise, Communications in Computational Physics, 26, (2019), 1335-1364. PDF file
35. A third order exponential time differencing numerical scheme for no-slope-selection epitaxial thin film model with energy stability. K. Cheng, Z. Qiao, C. Wang, Journal of Scientific Computing, 81, (2019), 154-185. PDF file
36. Positivity-preserving, energy stable numerical schemes for the Cahn-Hilliard equation with logarithmic potential. W. Chen, C. Wang, X. Wang, S. Wise, Journal of Computational Physics: X, 3, (2019), 100031. PDF file
37. A positivity-preserving, energy stable and convergent numerical scheme for the Cahn-Hilliard equation with a Flory-Huggins-deGennes energy. L. Dong, C. Wang, H. Zhang, Z. Zhang, Communications in Mathematical Science, 17, (2019), 921-939. PDF file
38. A weakly nonlinear energy stable scheme for the strongly anisotropic Cahn-Hilliard system and its convergence analysis. K. Cheng, C. Wang, S. Wise, Journal of Computational Physics, 405 (2020), 109109. PDF file
39. A stabilized second order ETD multistep method for thin film growth model without slope selection. W. Chen, W. Li, Z. Luo, C. Wang, X. Wang, Mathematical Modeling and Numerical Analysis, M2AN, 54 (2020), 727-750. PDF file
40. Optimal rate convergence analysis of a second order scheme for a thin film model with slope selection. S. Wang, W. Chen, H. Pan, C. Wang, Journal of Computational and Applied Mathematics, 377 (2020), 112855. PDF file
41. Energy stable numerical schemes for Ternary Cahn-Hilliard system. W. Chen, C. Wang, S. Wang, X. Wang, S. Wise, Journal of Scientific Computing, 84 (2020), 27. PDF file
42. Energy stable higher order linear ETD multi-step methods for gradient flows: application to thin film epitaxy. W. Chen, W. Li, C. Wang, S. Wang, X. Wang, Research in the Mathematical Sciences, 7 (2020), 13. PDF file
43. Global-in-time Gevrey regularity solutions for the functionalized Cahn-Hilliard equation. K. Cheng, C. Wang, S. Wise, Z. Yuan, Discrete and Continuous Dynamical Systems-Series S, 13 (2020), 2211-2229. PDF file
44. A positivity-preserving second-order BDF scheme for the Cahn-Hilliard equation with variable interfacial parameters. L. Dong, C. Wang, H. Zhang, Z. Zhang, Communications in Computational Physics, 28 (2020), 967-998. PDF file
45. Numerical comparison of modified-energy stable SAV-type schemes and classical BDF methods on benchmark problems for the functionalized Cahn-Hilliard equation. C. Zhang, J. Ouyang, C. Wang, S. Wise, Journal of Computational Physics, 423 (2020), 109772. PDF file
46. Artificial regularization parameter analysis for the no-slope-selection epitaxial thin film model. X. Meng, Z. Qiao, C. Wang, Z. Zhang, CSIAM Transaction on Applied Mathematics, 1 (2020), 441-462. PDF file
47. Artificial regularization parameter analysis for the no-slope-selection epitaxial thin film model. X. Meng, Z. Qiao, C. Wang, Z. Zhang, CSIAM Transaction on Applied Mathematics, 1 (2020), 441-462. PDF file
48. Convergence analysis for a stabilized linear semi-implicit numerical scheme for the nonlocal Cahn-Hilliard equation. X. Li, Z. Qiao, C. Wang, Mathematics of Computation, 90 (2021), 171-188. PDF file
49. A positive and energy stable numerical scheme for the Poisson-Nernst-Planck-Cahn-Hilliard equations with steric interactions. Y. Qian, C. Wang, S. Zhou, Journal of Computational Physics, 426 (2021), 109908. PDF file
50. An improved error analysis for a second-order numerical scheme for the Cahn-Hilliard equation. J. Guo, C. Wang, S. Wise, X. Yue, Journal of Computational and Applied Mathematics, 388 (2021), 113300. PDF file
51. A third order BDF energy stable linear scheme for the no-slope-selection thin film model. Y. Hao, Q. Huang, C. Wang, Communications in Computational Physics, 29 (3) (2021), 905-929. PDF file
52. A structure-preserving, operator splitting scheme for reaction-diffusion equations with detailed balance. C. Liu, C. Wang, Y. Wang, Journal of Computational Physics, 436 (2021), 110253. PDF file
53. Structure-preserving, energy stable numerical schemes for a liquid thin film coarsening model. J. Zhang, C. Wang, S. Wise, Z. Zhang, SIAM Journal on Scientific Computing, 43 (2) (2021), A1248-A1272. PDF file
54. A positivity-preserving and convergent numerical scheme for the binary fluid-surfactant system. Y. Qin, C. Wang, Z. Zhang, International Journal of Numerical Analysis and Modeling, 18 (3) (2021), 399-425. PDF file
55. An energy stable finite element scheme for the three-component Cahn-Hilliard-type model for macromolecular microsphere composite hydrogels. M. Yuan, W. Chen, C. Wang, S. Wise, Z. Zhang, Journal of Scientific Computing, 87 (2021), 78. PDF file
56. A positivity preserving, energy stable scheme for the ternary Cahn-Hilliard system with the singular interfacial parameters. L. Dong, C. Wang, S. Wise, Z. Zhang, Journal of Computational Physics, 442, (2021), 110451. PDF file
57. A second order accurate scalar auxiliary variable (SAV) numerical method for the square phase field crystal equation. M. Wang, Q. Huang, C. Wang, Journal of Scientific Computing, 88 (2) (2021), 33. PDF file
58. A positivity-preserving, energy stable and convergent numerical scheme for the Poisson-Nernst-Planck system. C. Liu, C. Wang, S. Wise, X. Yue, S. Zhou, Mathematics of Computation, 90 (2021), 2071-2106. PDF file
59. Error estimate of second order accurate scalar auxiliary variable (SAV) scheme for the thin film epitaxial models. Q. Cheng, C. Wang, Advances in Applied Mathematics and Mechanics, 13 (2021), 1318-1354. PDF file
60. A modified Crank-Nicolson scheme for the Flory-Huggins Cahn-Hilliard model. W. Chen, J. Jing, C. Wang, X. Wang, S. Wise, Communications in Computational Physics, 31 (1) (2022), 60-93. PDF file
61. An iteration solver for the Poisson-Nernst-Planck system and its convergence analysis. C. Liu, C. Wang, S. Wise, X. Yue, S. Zhou, Journal of Computational and Applied Mathematics, 406 (2022), 114017. PDF file
62. A third order accurate in time, BDF-type energy stable scheme for the Cahn-Hilliard equation. K. Cheng, C. Wang, S. Wise, Y. Wu, Numerical Mathematics: Theory, Methods and Applications, 15 (2) (2022), 279-303. PDF file
63. Convergence analysis of the variational operator splitting scheme for a reaction-diffusion system with detailed balance. C. Liu, C. Wang, Y. Wang, S. Wise, SIAM Journal on Numerical Analysis, 60 (2) (2022), 781-803. PDF file
64. A positivity preserving, energy stable finite difference scheme for the Flory-Huggins-Cahn-Hilliard-Navier-Stokes system. W. Chen, J. Jing, C. Wang, X. Wang, Journal of Scientific Computing, 92 (2022), 31. PDF file
65. Optimal rate convergence analysis of a numerical scheme for the ternary Cahn-Hilliard system with a Flory-Huggins-deGennes energy potential. L. Dong, C. Wang, S. Wise, Z. Zhang, Journal of Computational and Applied Mathematics, 406 (2022), 114474. PDF file
66. Error estimate of a decoupled numerical scheme for the Cahn-Hilliard-Stokes-Darcy system. W. Chen, D. Han, C. Wang, S. Wang, X. Wang, Y. Zhang, IMA Journal of Numerical Analysis, 42 (3) (2022), 2621-2655. PDF file
67. A second order accurate, operator splitting schemes for reaction-diffusion systems in the energetic variational formulation. C. Liu, C. Wang, Y. Wang, SIAM Journal on Scientific Computing, 44 (4) (2022), A2276-A2301. PDF file
68. A second order accurate in time, energy stable finite element scheme for the Flory-Huggins-Cahn-Hilliard equation. M. Yuan, W. Chen, C. Wang, S. Wise, Z. Zhang, Advances in Applied Mathematics and Mechanics, 14 (6) (2022), 1477-1508. PDF file
69. A preconditioned steepest descent solver for the Cahn-Hilliard equation with variable mobility. X. Chen, C. Wang, S. Wise, International Journal of Numerical Analysis and Modeling, 19 (6) (2022), 839-863. PDF file
70. A thermodynamically-consistent phase field crystal model of solidification with heat flux. C. Wang, S. Wise, Journal of Mathematical Study, 55 (2022), 337-357. PDF file
71. Convergence analysis of structure-preserving numerical methods based on Slotboom transformation for the Poisson-Nernst-Planck equations. J. Ding, C. Wang, S. Zhou, Communications in Mathematical Sciences, 21 (2) (2023), 459-484. PDF file
72. Convergence analysis on a structure-preserving numerical scheme for the Poisson-Nernst-Planck-Cahn-Hilliard system. Y. Qian, C. Wang, S. Zhou, CSIAM Transaction on Applied Mathematics, 4 (2) (2023), 345-380. PDF file
73. An energy stable finite difference scheme for the Ericksen-Leslie system with penalty function and its optimal rate convergence analysis. K. Cheng, C. Wang, S. Wise, Communications in Mathematical Sciences, 21 (4) (2023), 1135-1169. PDF file
74. Stabilization parameter analysis of a second order linear numerical scheme for the nonlocal Cahn-Hilliard equation. X. Li, Z. Qiao, C. Wang, IMA Journal of Numerical Analysis, 43 (2) (2023), 1089-1114. PDF file
75. High order accurate and convergent numerical scheme for the strongly anisotropic Cahn-Hilliard mode. K. Cheng, C. Wang, S. Wise, Numerical Methods for Partial Differential Equations, 39 (2023), 4007-4029. PDF file
76. A second order accurate, positivity preserving numerical method for the Poisson-Nernst-Planck system and its convergence analysis. C. Liu, C. Wang, S. Wise, X. Yue, S. Zhou, Journal of Scientific Computing, 97 (1) (2023), 23. PDF file
77. Convergence analysis of a temporally second-order accurate finite element scheme for the Cahn-Hilliard-magnetohydrodynamics system of equations. C. Wang, J. Wang, S. Wise, Z. Xia, L. Xu, Journal of Computational and Applied Mathematics, 436 (2024), 115409. PDF file
78. Double stabilizations and convergence analysis of a second-order linear numerical scheme for the nonlocal Cahn-Hilliard equation. X. Li, Z. Qiao, C. Wang, Science China Mathematics, 67 (1) (2024), 187-210. PDF file
79. A scalar auxiliary variable (SAV) finite element numerical scheme for the Cahn-Hilliard-Hele-Shaw system with dynamic boundary conditions. C. Yao, F. Zhang, C. Wang, Journal of Computational Mathematics, 42 (2) (2024), 544-569. PDF file
80. A second order accurate, positivity-preserving numerical scheme of the Cahn-Hilliard-Navier-Stokes system with Flory-Huggins potential. W. Chen, J. Jing, Q. Liu, C. Wang, X. Wang, Communications in Computational Physics, 35 (2024), 633-661. PDF file
81. Convergence analysis of a second order numerical scheme for the Flory-Huggins-Cahn-Hilliard-Navier-Stokes system. W. Chen, J. Jing, Q. Liu, C. Wang, X. Wang, Journal of Computational and Applied Mathematics, 450 (2024), 115981. PDF file
82. A third order positivity-preserving, energy stable numerical scheme for the Cahn-Hilliard equation with logarithmic potential. Y. Li, J. Jing, Q. Liu, C. Wang, W. Chen, Science China Mathematics, Chinese version, 54 (2024), 1-30. PDF file
83. Convergence analysis of a positivity-preserving numerical scheme for the Cahn-Hilliard-Stokes system with Flory-Huggins energy potential. Y. Guo, C. Wang, S. Wise, Z. Zhang, Mathematics of Computation, 93 (349) (2024), 2185-2214. PDF file
84. Efficient finite element schemes for a phase field model of two-phase incompressible flows with different densities. J. Wang, M. Li, C. Wang, Journal of Computational Physics, 518 (2024), 113331. PDF file
85. A refined convergence estimate for a fourth order finite difference numerical scheme to the Cahn-Hilliard equation. J. Guo, C. Wang, Y. Yan, X. Yue, Advances in Applied Mathematics and Mechanics, (2024), accepted and in press. PDF file
86. Convergence analysis of a preconditioned steepest descent solver for the Cahn-Hilliard equation with logarithmic potential. A. Diegel, C. Wang, S. Wise, International Journal of Numerical Analysis and Modeling, (2024), accepted and in press. PDF file
87. On a positive-preserving, energy-stable numerical scheme to mass-action kinetics with detailed balance. C. Liu, C. Wang, Y. Wang, Communications in Mathematical Sciences, (2024), submitted and in review.
88. Global-in-time energy stability analysis for the exponential time differencing Runge-Kutta scheme for the phase field crystal equation. X. Li, Z. Qiao, C. Wang, Mathematics of Computation, (2024), submitted and in review.
89. A positivity-preserving, second-order energy stable and convergent numerical scheme for a ternary system of macromolecular microsphere composite hydrogels. L. Dong, C. Wang, Z. Zhang, Journal of Computational and Applied Mathematics, (2024), submitted and in review.
90. Unique solvability and error analysis of the Lagrange multiplier approach for gradient flows. Q. Cheng, J. Shen, C. Wang, SIAM Journal on Numerical Analysis, (2024), submitted and in review.
91. A second-order accurate, structure preserving numerical scheme for the Poisson-Nernst-Planck-Navier-Stokes (PNPNS) system. Y. Qin, C. Wang, IMA Journal of Numerical Analysis, (2024), submitted and in review.
92. A second-order, original energy dissipative numerical scheme for chemotaxis and its convergence analysis. J. Ding, C. Wang, S. Zhou, Mathematics of Computation, (2024), submitted and in review.
93. A uniquely solvable and positivity-preserving finite difference scheme for the Flory-Huggins-Cahn-Hilliard equation with dynamical boundary condition. Y. Guo, C. Wang, S. Wise, Z. Zhang, Journal of Computational and Applied Mathematics, (2024), submitted and in review.
94. Maximum bound principle and bound preserving ETD schemes for a phase-field model of tumor growth with extracellular matrix degradation. Q. Huang, Z. Qiao, C. Wang, H. Yang, Mathematical Models and Methods in Applied Sciences, (2024), submitted and in review.
95. A third order accurate, energy stable exponential time differencing multi-step scheme for Landau-Brazovskii model. M. Cui, Y. Niu, C. Wang, Z. Xu, (2024), in preparation.
96. Convergence analysis for a reaction-diffusion system with nonlinear diffusion process. C. Liu, C. Wang, Y. Wang, S. Wise, (2024), in preparation.
97. Convergence analysis of a second order accurate, operator splitting scheme for the energetic variational approach of reaction-diffusion system. C. Liu, C. Wang, Y. Wang, S. Wise, (2024), in preparation.
98. A positivity-preserving, energy stable numerical scheme for the energetic variational approach of reaction-diffusion-Stokes system. C. Liu, C. Wang, Y. Wang, S. Wise, (2024), in preparation.
99. A positivity preserving, entropy increasing numerical scheme for the thermodynamically-consistent model of phase field crystal equation. C. Liu, C. Wang, Y. Wang, S. Wise, (2024), in preparation.
100. A third order accurate, linear energy stable BDF3 numerical scheme for non-local Cahn-Hilliard equation. Q. Huang, Z. Qiao, C. Wang, (2024), in preparation.
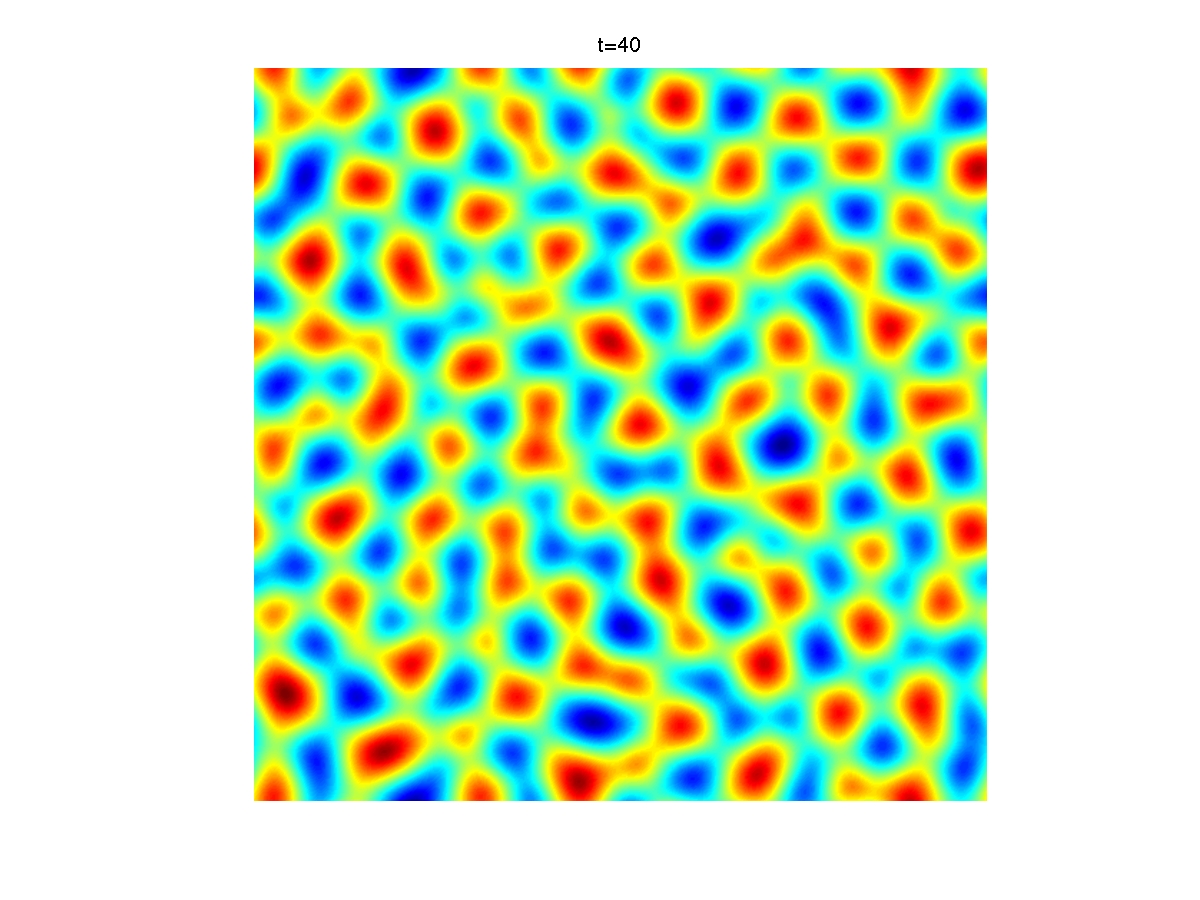
Epitaxial thin film growth without slope selection

Please send any comments or suggestions to: cwang1@umassd.edu, 12/06/24