My research work in this direction is focused on the subject of CFD (computational fluid dynamics), which is the design and analysis of numerical methods to approximate incompressible flow as described by the Navier-Stokes Equations (NSE).

There has been a tremendous amount of work on this subject in the past. Some well-known difficulties, such as enforcement of the incompressibility constraint, lack of a dynamic equation and a boundary condition for the pressure, and implementation of the vorticity boundary condition, have existed for both the primitive variable formulation and the vorticity formulation. In addition, one faces serious challenges in dealing with a flow with a high Reynolds number, due to the sharp gradient of the flow, lack of resolution and inefficiency of the numerical scheme. Furthermore, the application of many classical high order methods (such as spectral methods) to a numerical example with a non-periodic boundary condition may lead to a high computational cost, and spurious effects are often observed. Stability presents another big concern for these classical approaches.

In a sequence of my articles, new approaches were proposed and implemented to overcome the above-mentioned difficulties. In particular, the proposed numerical schemes avoid a Stokes solver, using only a Poisson solver at each time step (stage). As a result, these schemes are highly efficient and are capable of producing highly resolved solutions for complicated structural transitions of the flow at a reasonable computational cost. Moreover, spurious effects or numerical artifacts around the boundary, due to the stability and accuracy of the scheme, are not observed.

Similar ideas can be applied to deal with geophysical flows, such as the Primitive Equations (PEs) and the Planetary Geostrophic Equations (PGEs), and the 3-D Quasi-Geostrophic equations (QGEs). These models represent the fundamental governing equations for atmospheric and oceanic flow under different physical scales. A special property for the horizontal velocity field, which is a nonlocal constraint, reflects the fact that the flow with large scale or mesoscale is essentially two-dimensional. This makes possible the efficient solution of these equations avoiding the numerical difficulties which typically arise in three-dimensional flows.

The PEs can be formulated in either surface pressure Poisson equation or mean vorticity. Both 3-D staggered MAC (marker and cell) grids and regular numerical grids are extensively discussed, with both second and fourth order accuracy. The PGEs with inviscid geostrophic balance are formulated in an alternate form.

Moreover, collocation spectral methods can be applied to deal with GFD models, with a careful treatment of hydrostatic and geostrophic balance equations. The purpose for utilizing these high order methods is to improve the accuracy within the limited resolution due to the enormous scale of the three-dimensional setting. The calculation of thermocline evolution in large scale oceanic motion was also undertaken.

Direct impacts of the numerical methods include more detailed simulation of weather systems (both global and local), and more efficient use of supercomputer resources. If successful, a better understanding of the detailed process of weather dynamics is expected due to the efficiency of the reformulations and the high accuracy and stability of the proposed methods.

As another application, these numerical schemes can be used to study the structural stability and bifurcation of incompressible fluid. Solutions of the incompressible fluid equations in different physical formulations, either NSE, Boussinesq equations, or other physical models, can be viewed as one-parameter families of divergence-free vector fields with time as the parameter. The structural analyses of divergence-free velocity vector fields, including topological equivalence classes, stability conditions, and structural bifurcation criterion, have attracted much attention. Such analyses can be carried out both theoretically and numerically. Some theoretical results were recently obtained in related references. My work in this direction is focused to a detailed numerical study of both structural stability and structural bifurcation, i.e., change of topological equivalence class, for 2-D incompressible flow under different physical set-ups.

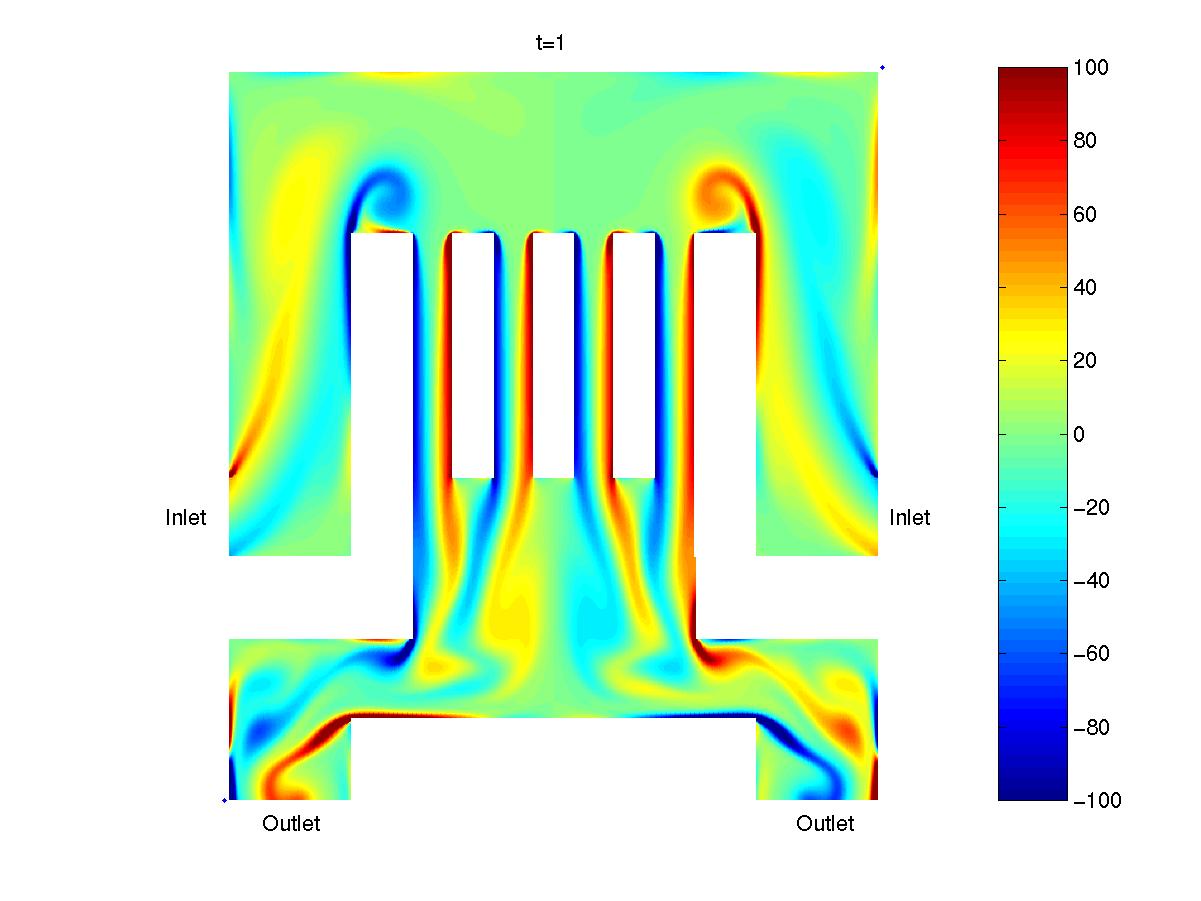
Flow in a cooling system

Please send any comments or suggestions to: cwang1@umassd.edu, 12/02/24