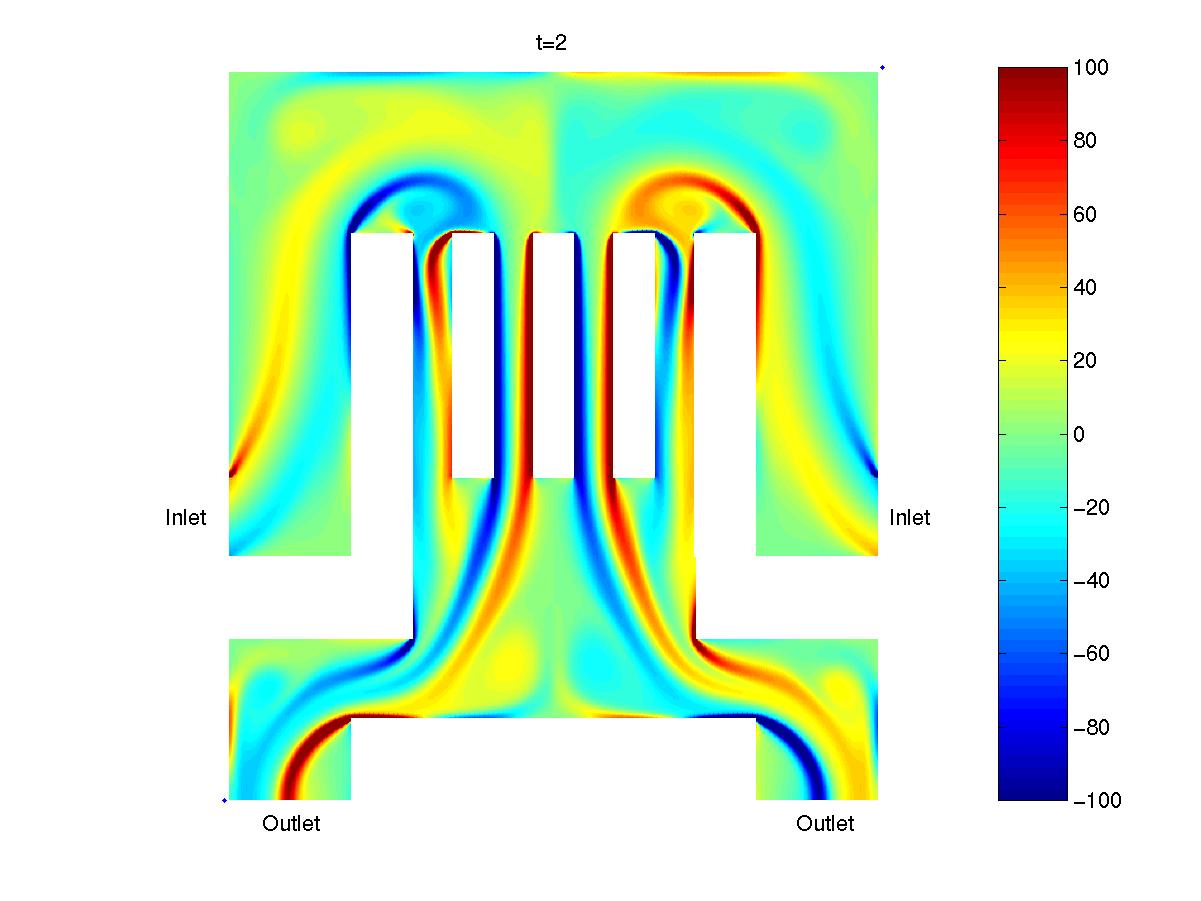
The above figure is a visualization of
the vorticity profile at time t=2 of
incompressible flow passing through a cooling system.
The Reynolds number is taken to be 2000.
Such flow motion can be
described as incompressible Navier-Stokes equations. We use a compact
fourth order method to simulate such process.
Only two poisson solvers are needed at each Runge-Kutta time stage.
The no-slip boundary condition for the velocity is converted into
high order boundary condition for the vorticity, such as Briley's
formula. The main difficulty and trick lies in the Poisson
solvers, because of the complexity of the flow region.
The numerical experimant shows that Schwarz iteration plus FFT
gives an excellent convergence result for the poisson solvers.
