A. Heryudono, R. J. Braun, T. A. Driscoll, K. L. Maki, L. P. Cook, and P. E. King-Smith.
Single-equation models for the tear film in
a blink cycle: realistic lid motion
Mathematical Medicine and Biology, Vol 24, Issue 4, 2007.
In collaboration with Richard Braun, Toby Driscoll and with support from NSF Grant #DMS-0616483, I am working on the implementation of spectral methods and adaptive RBF methods to solve a fourth-order nonlinear equation arising as a model of the blink cycle process in human eyes.
Tear Film Presentation at APS DFD Meeting .
Tear Film Presentation at George Mason University .
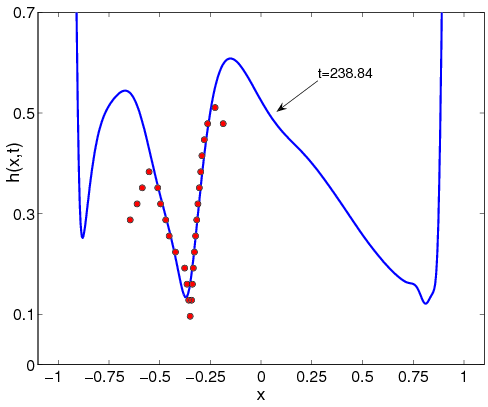
We study the dynamics of the tear film on the human eye, the main form of protection for the open eye. We combined physical modeling and analytical techniques to derive the simplest nonlinear partial differential equation (with appropriate boundary and initial conditions) that are appropriate for the problem. The equations to be solved determine the tear film thickness along a vertical line. Some results are shown as the solid curve in Figure below.

The mathematical results are compared with experimentally measured tear film thickness on the front of a contact lens. Figure below shows interference fringes which indicate changes in the thickness of the tear film; combined with a second imaging technique, the actual tear film thickness can be computed. Tear film thickness along the dark vertical line is compared with theoretical results computed from the mathematical model.

The film is shown after a "half blink" in both the experiment and the mathematical model. Many blinks are only partial; the upper lid doesn't completely close. In the case we are comparing here, the upper lid came halfway down and then fully opened. The tear film thickness shows that which occurs when the lid just finished opening. The upper lid left a valley in the tear film, which is predicted by the theory. The theory captures some but not all of the features of the valley; improvements in the mathematical model are currently underway.