Scott Field
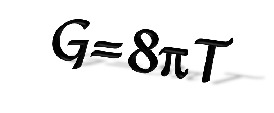
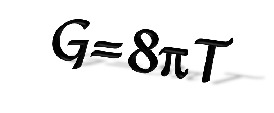
For the most up-to-date view of what we are working on, please see our recent publications.
Broadly speaking, our research group focuses on building gravitational wave models for precessing, eccentric, and high-mass ratio systems, and then using these models to analyze gravitational-wave datasets. We are also involved with the numerical simulation of binary black hole systems. Our work is a mixture of gravitational-wave science, designing numerical algorithms, and writing open-source software.
Some of our work was recently featured in Quanta!
Images: SXS Collaboration
Parameterized gravitational wave models, from the Einstein equation to closed-form post-Newtonian approximations, carry an evaluation cost. These costs constitute a major bottleneck for many important applications which can require thousands or millions of model evaluations. For example, binary blackhole sources are parameterized by 8 degrees of freedom; each orbiting blackhole has 1 mass and 3 spin degrees of freedom. In turn each simulation of the Einstein equation often requires weeks on large supercomputing clusters. On the other hand, repeated model evaluations are required by parameter estimation (i.e. inverse) problems. The high simulation cost currently prevents parameter estimation from being carried out with gravitational waveforms found by way of the Einstein equation. For upcoming gravitational wave experiments, parameter estimation studies are expected to take months for low-fidelity models, while being altogether impractical for more faithful models.
Markov chain Monte Carlo (MCMC) algorithms are a commonly used technique for sampling the posterior probability distribution function. When dealing with high dimensional problems, however, the process of mapping the posterior can become prohibitively expensive. Additionally, the posterior is multimodal and the gravitational wave signal is buried in detector noise, thereby rendering otherwise useful computational tricks ineffective. For example, millions of degrees of freedom characterize a typical advanced detector dataset, and equally long MCMC chains are necessary to compute parameter means and variances. In total, from model evaluations one should expect to generate around one Petabyte per analysis. Such data science challenges constitute a major computational bottleneck of the experiment and are among the most pressing questions in gravitational wave parameter estimation.
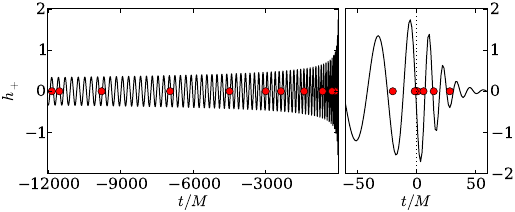
Image: Surrogate GW model
To overcome these challenges I have been involved in a long-term research program to develop and apply surrogate and reduced order modeling tools for both the rapid evaluation of gravitational waveforms and rapid parameter estimation using “compressed” likelihoods. These results rely upon identification of a low-dimensional representation for a given waveform family which in turn forms the building blocks for fast, scalable algorithms. For more information about this research please visit these websites on reduced order modeling for gravitational waves, reduced order quadratures for accelerated Bayesian inference and surrogate models.
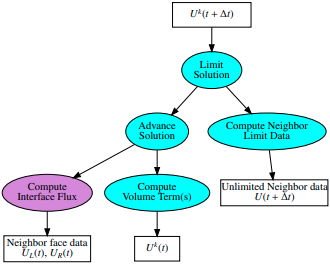
Images: Task dependency graph of a DG method
To handle a diverse class of astrophysical sources in an efficient, robust and accurate manner, the development of advanced and flexible methods is paramount. Discontinuous Galerkin (DG) methods have the potential to offer unique benefits for a wide class of problems. We have developed DG methods for the first-order and second-order BSSN system (a numerically well-suited formulation of the Einstein equation) which achieve spectral accuracy (i.e. exponential convergence of numerical errors) and long-time stability. These implementations should provide a starting point for treating both fluid and spacetime variables with the same high-order accurate DG method.
In the context of extreme mass ratio (binary black hole) inspiral systems the solutions are forced by distributional (i.e. Dirac delta function) source terms. We proposed and implemented a DG scheme to exactly represent such distributional solutions through a modification of the relevant numerical flux terms. Furthermore, it was demonstrated that the method maintains spectral accuracy even at the location of the Dirac delta distribution. Accurate numerical modeling is crucial for the incorporation of important physical effects neglected by linearization such as the gravitational self-force.
Time-domain wave simulation on a finite computational domain introduces an outer boundary beyond which the solution is unknown. Whether for acoustic, electromagnetic, or gravitational waves one often seeks to identify the asymptotic signal radiated to the far-field using only knowledge of the solution on this truncated, spatially finite, computational domain. To solve this challenge in the context of blackhole perturbation theory we analytically identify and numerically construct a kernel which, when convolved with data recorded at a fixed radial value, yields the asymptotic signal. We applied the construction to the linearized Einstein equation and compute far-field, scri-waveforms from arbitrarily short computational domains with better than 10 digits of accuracy. Further details on this method as well as the publicly available numerical kernels can be found on the kernel webpage.