Lecture 4. Things to do in class.
Our goal is to solve 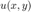 on the domain
on the domain ![$[-1,1] \times [-1,1]$](mth572lecture4_eq16896893380415760150.png) of the 2D Poisson Equation
of the 2D Poisson Equation
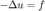
in 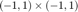 , where
, where
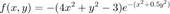
and
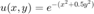
at the boundaries.
Contents
Number 1
- Get 1D version of 2nd-order 2nd-derivative differentiation matrix. For this particular problem, since
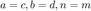 and
and 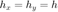 , we can use the same 1D 2nd-derivative differentiation matrix, i.e Dxx = Dyy = D2. Watch out for "un-centered" stencil weights.
, we can use the same 1D 2nd-derivative differentiation matrix, i.e Dxx = Dyy = D2. Watch out for "un-centered" stencil weights.
clear all; close all; % clear all to start fresh format long e % format number in long format a = -1; b = 1; n = 10; h = (b-a)/(n-1); one = ones(n,1); % create a column vector of size n by 1 of ones D2 = spdiags([one -2*one one],[-1 0 1],n,n); D2(1,1:4) = [2 -5 4 -1]; D2(end,end-3:end) = [-1 4 -5 2]; % Modify first and last row (one-sided weights) D2 = (1/h^2)*D2; % Don't forget the 1/(h^2) factor spy(D2) % Plot the structure of the sparse matrix
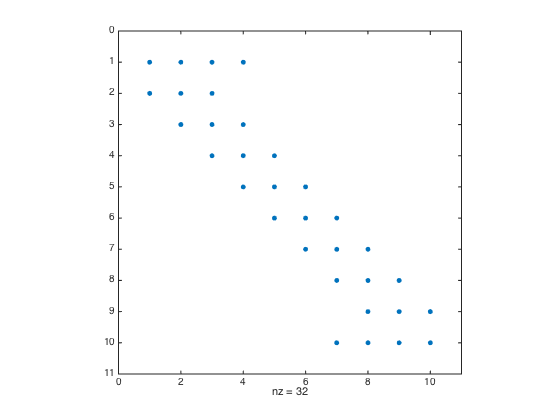
- Create Tensor Product Grid
x = linspace(a,b,n).'; % Create n equally-spaced points in [a,b] y = x; % set y = x [X,Y] = meshgrid(x,y); figure mesh(X,Y,0*X); view(2); % plot the grid hold on;
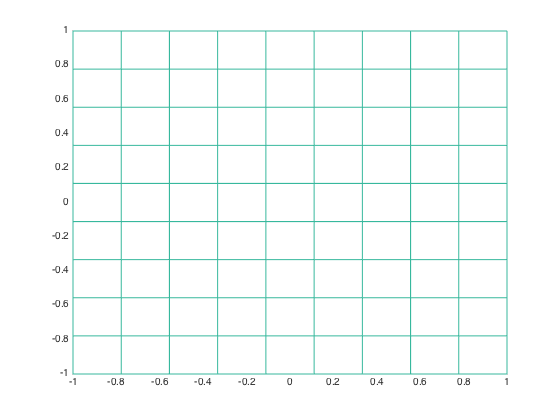
- Flag boundary points and plot them on the grid
flagbdr = true(size(X)); flagbdr(2:end-1,2:end-1) = false; % flag interior points as false plot(X(flagbdr),Y(flagbdr),'o','MarkerFaceColor','k','MarkerSize',8) xlabel('x'); ylabel('y');
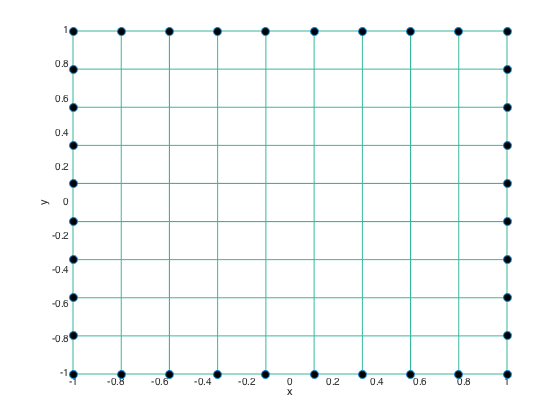
- Define the forcing and boundary condition functions and their discrete values
u = @(x,y) exp(-(x.^2+0.5*y.^2)); % Define the BC function (also happens to be the exact solution) f = @(x,y) -(4*x.^2 + y.^2 - 3).*exp(-(x.^2 +0.5*y.^2)); % Forcing function F = f(X,Y); F(flagbdr) = u(X(flagbdr),Y(flagbdr)); % at boundary nodes, replace rhs values. F = F(:); % vectorize F
- Create Laplacian differentiation matrix L = Dxx + Dyy.
I = speye(n); % Create sparse identity matrix
L = -(kron(D2,I) + kron(I,D2));
- Modify rows that correspond to boundary conditions (row replacement) and plot the matrix L
bdridx = find(flagbdr(:)); % get the linear indices of boundary nodes L(bdridx,:) = 0; % Set the boundary rows to zeros idx = sub2ind(size(L),bdridx,bdridx); L(idx) = 1; % set 1 to the diagonal entries of boundary rows figure; spy(L); % plot L
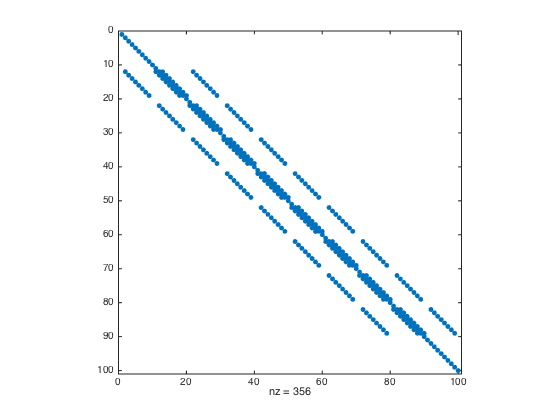
- Solve U and compare with the exact solution
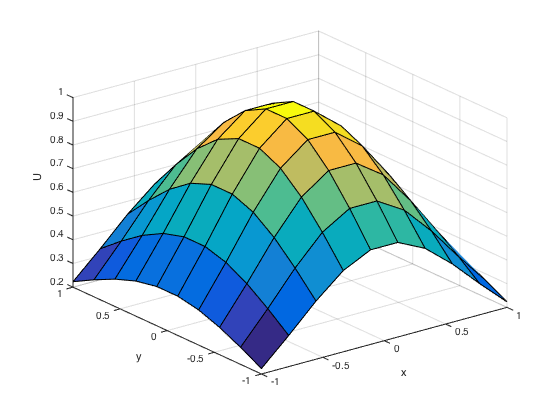
U = L\F; norm(U-u(X(:),Y(:)),Inf) U = reshape(U,n,n); figure surf(X,Y,U); xlabel('x'); ylabel('y'); zlabel('U');
ans =
8.733515070539877e-03
Number 2
- Perform Cuthill-McKee Permutation to the modified matrix L
P = symrcm(L); spy(L(P,P))
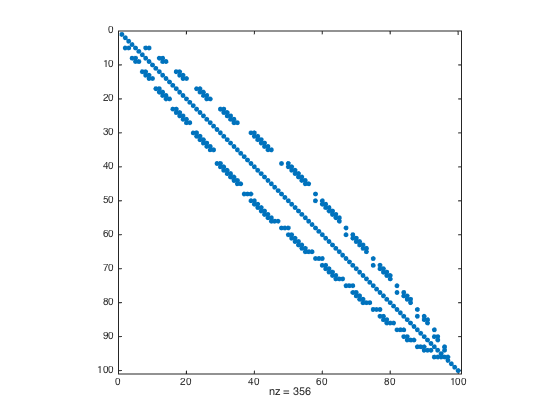
- Solve U and compare with the exact solution
U = zeros(size(F)); U(P) = L(P,P)\F(P); norm(U-u(X(:),Y(:)),Inf)
ans =
8.733515070539877e-03
- Instead of using backslash \, you also use one of the iterative solvers that you learned in numerical linear algebra such as gmres for non symmetric matrix.
U = zeros(size(F));
MAXITER = 20; TOL = 1e-13; RESTART = []; % No restart.
[U(P),FLAG,RELRES,ITER,RESVEC] = gmres(L(P,P),F(P),RESTART,TOL,MAXITER);
norm(U-u(X(:),Y(:)),Inf)
ans =
8.733515070537212e-03
- Plot the residual convergence of the gmres
semilogy(1:length(RESVEC),RESVEC/norm(F(P)),'-o','markerfacecolor','k','markersize',8); xlabel('Iteration number'); ylabel('Relative residual');
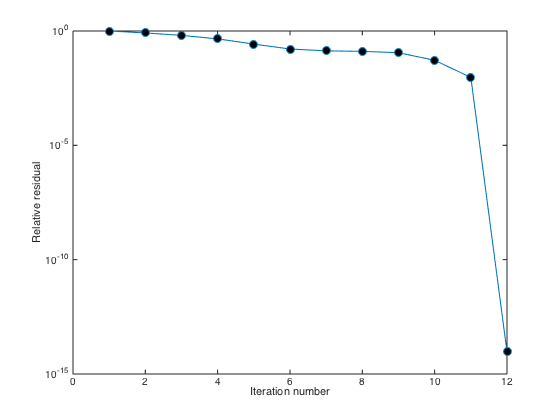
Without restarting, the gmres iteration converges in 12 iterations and the residual suddenly drops from iteration 11 to iteration 12. However, you can also try to pre-condition the matrix L with Incomplete LU decomposition.
U = zeros(size(F)); MAXITER = 20; TOL = 1e-13; RESTART = []; % No restart. [ML,MU] = ilu(L(P,P),struct('type','ilutp','droptol',1e-6)); % Get the preconditioners. [U(P),FLAG,RELRES,ITER,RESVEC] = gmres(L(P,P),F(P),RESTART,TOL,MAXITER,ML,MU); norm(U-u(X(:),Y(:)),Inf) hold on semilogy(1:length(RESVEC),RESVEC/norm(F(P)),'-*','markerfacecolor','r','markersize',8);
ans =
8.733515070539766e-03
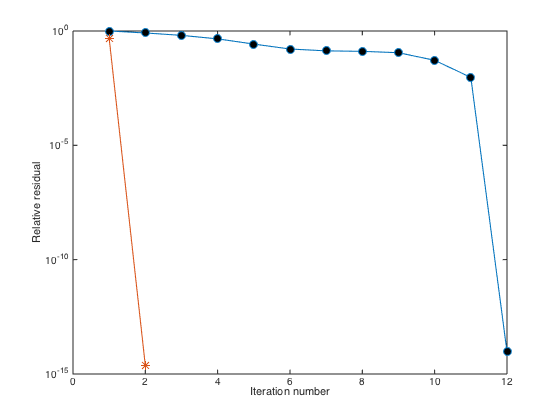
It turns out that the gmres iteration for the pre-conditioned system converges with only 2 iterations. Try to increase the size n to 60 instead of 10.
Number 3
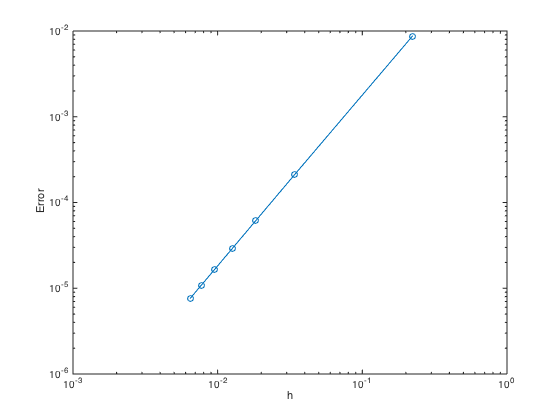
For 2nd order convergence, slope of the error convergence must be 2.
n = 10:50:310; % Create n = 10,110,210,310,... h = (b-a)./(n-1); err = zeros(length(n),1); % Pre-allocate memory to store errors for i=1:length(n) one = ones(n(i),1); D2 = spdiags([one -2*one one],[-1 0 1],n(i),n(i)); D2(1,1:4) = [2 -5 4 -1]; D2(end,end-3:end) = [-1 4 -5 2]; D2 = (1/h(i)^2)*D2; x = linspace(a,b,n(i)).'; y = x; % set y = x [X,Y] = meshgrid(x,y); flagbdr = true(size(X)); flagbdr(2:end-1,2:end-1) = false; F = f(X,Y); F(flagbdr) = u(X(flagbdr),Y(flagbdr)); F = F(:); I = speye(n(i)); L = -(kron(D2,I) + kron(I,D2)); bdridx = find(flagbdr(:)); L(bdridx,:) = 0; idx = sub2ind(size(L),bdridx,bdridx); L(idx) = 1; U = L\F; err(i) = norm(U-u(X(:),Y(:)),Inf); end figure loglog(h,err,'-o') % Plot the errors in logscale xlabel('h'); ylabel('Error')