Lecture2. Things to do in class.
Contents
Testing 2nd order derivative with problems (1)-(3) from Lecture 1
- Redo Number 1 in Lecture 1 with 2nd-order differentiation matrix
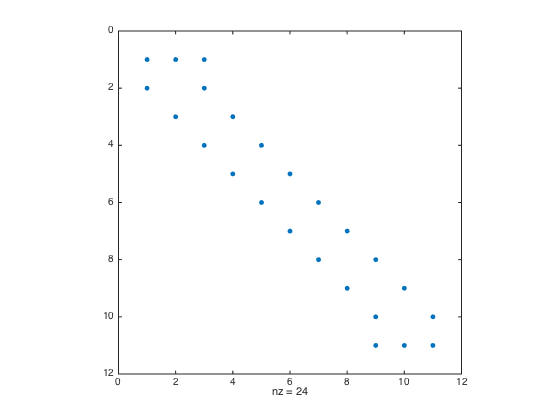
clear all; close all; % clear all to start fresh % Note: n equal spacing means n+1 points % as an example let use use a = -1 and b = 1 a = -1; b = 1; n = 10; h = (b-a)/n; one = ones(n+1,1); % create a column vector of size n+1 by 1 of ones D = spdiags([-one one],[-1 1],n+1,n+1); D(1,1:3) = [-3 4 -1]; D(end,end-2:end) = [1 -4 3]; % Modify first and last row (one-sided weights) D = (0.5/h)*D; % Don't forget the 1/(2*h) factor spy(D) % Plot the structure of the sparse matrix
- Redo Number 2 in Lecture 1 with 2nd-order differentiation matrix
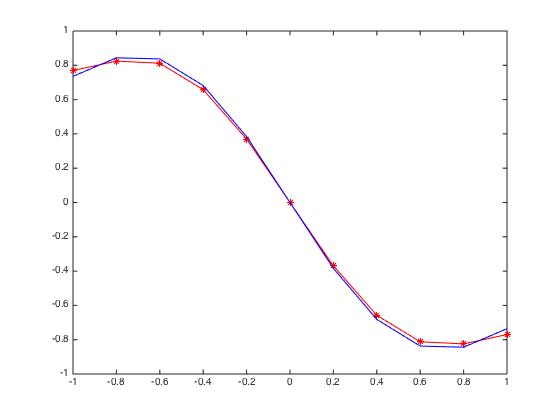
format long e % format number in long format u = @(x) exp(-x.^2); % Define the function ux = @(x) -2*x.*exp(-x.^2); % Define the exact derivative of the function x = linspace(a,b,n+1).'; % Create n+1 equally-spaced points in [a,b] uux = D*u(x); % Compute numerical derivative err = norm(uux-ux(x),Inf) % Compute infnorm (u'_num - u'_exact) figure plot(x,uux,'-*r',x,ux(x),'-b')
err =
3.387873412420639e-02
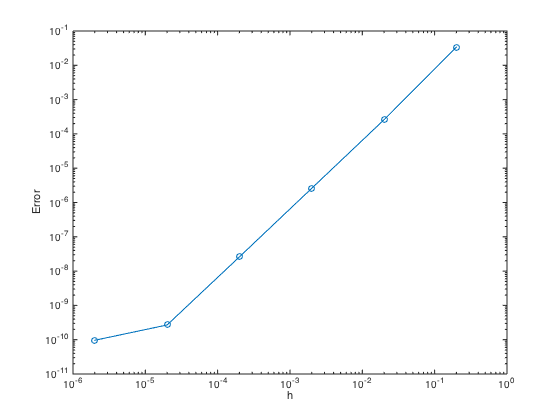
- Redo Number 3 in Lecture 1 with 2nd-order differentiation matrix Can you check what is the slope of the error convergence ? Any idea why the error is somewhat level off when h is getting smaller ?
n = 10.^(1:6); % Create n = 10,100,1000,10000,... h = (b-a)./n; err = zeros(length(n),1); % Pre-allocate memory to store errors for i=1:length(n) one = ones(n(i)+1,1); x = linspace(a,b,n(i)+1).'; D = spdiags([-one one],[-1 1],n(i)+1,n(i)+1); D(1,1:3) = [-3 4 -1]; D(end,end-2:end) = [1 -4 3]; D = (0.5/h(i))*D; uux = D*u(x); err(i) = norm(uux-ux(x),Inf); end figure loglog(h,err,'-o') % Plot the error in logscale xlabel('h'); ylabel('Error')
Number 1
a = -1; b = 0.5; n = 20; h = (b-a)/n; x = linspace(a,b,n+1).'; gn = exp(-0.5); % boundary condition at x=0.5 f = @(x) (pi*cos(pi*x)-sin(pi*x)).*exp(-x); % Right hand side function one = ones(n+1,1); % create a column vector of size n+1 by 1 of ones
- Row Replacement Method
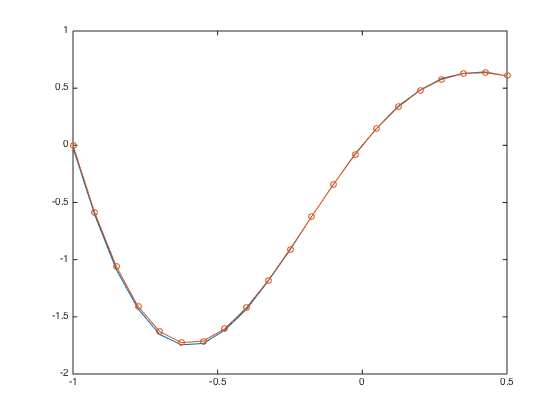
D = spdiags([-one one],[-1 1],n+1,n+1); D(1,1:3) = [-3 4 -1]; % modify 1st row due to one-sided difference D(end,end-2:end) = [0 0 2*h]; % Modify last row due to BC D = (0.5/h)*D; % Don't forget the 1/(2*h) factor F = f(x); % RHS vectors F(end) = gn; % Set last element of RHS vector to BC. u = D\F; % solve the system. uexact = @(x) sin(pi*x).*exp(-x); err = norm(u-uexact(x),Inf) plot(x,u,'-',x,uexact(x),'-o')
err =
2.633918963991388e-02
- Strip Row Move Over Column Method
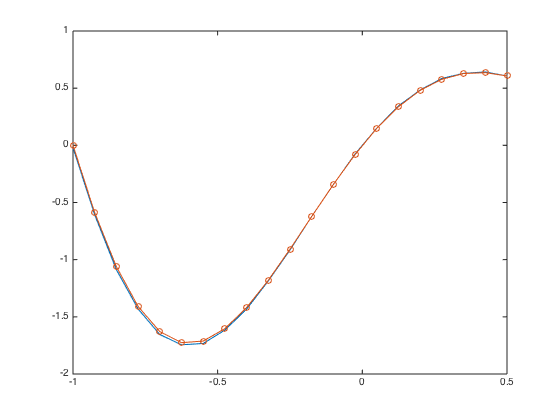
D = spdiags([-one one],[-1 1],n+1,n+1); D(1,1:3) = [-3 4 -1]; % modify 1st row due to one-sided difference D(end,:) = []; % Strip last row. D = (0.5/h)*D; % Don't forget the 1/(2*h) factor F = f(x(1:n)) - gn*D(:,end) ; % RHS vectors adjusted due to moved column D(:,end) = []; % Strip last column u = D\F; % solve the system. uexact = @(x) sin(pi*x).*exp(-x); u = [u;gn]; % err = norm(u-uexact(x),Inf) plot(x,u,'-',x,uexact(x),'-o')
err =
2.633918963991388e-02
Number 2
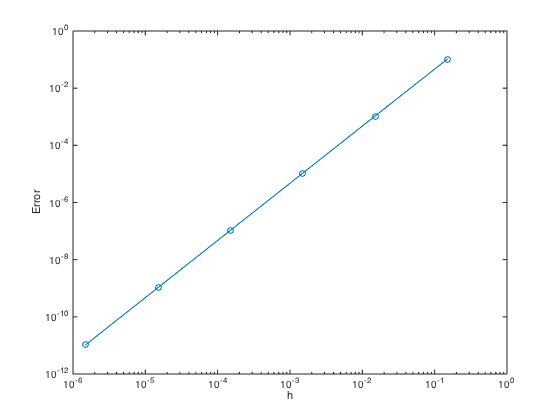
Test convergence by using Strip row move over column. Please do it also for the Row Replacement Method
n = 10.^(1:6); % Create n = 10,100,1000,10000,... h = (b-a)./n; err = zeros(length(n),1); % Pre-allocate memory to store errors uexact = @(x) sin(pi*x).*exp(-x); for i=1:length(n) one = ones(n(i)+1,1); x = linspace(a,b,n(i)+1).'; D = spdiags([-one one],[-1 1],n(i)+1,n(i)+1); D(1,1:3) = [-3 4 -1]; % modify 1st row due to one-sided difference D(end,:) = []; % Strip last row. D = (0.5/h(i))*D; % Don't forget the 1/(2*h) factor F = f(x(1:n(i))) - gn*D(:,end) ; % RHS vectors adjusted due to moved column D(:,end) = []; % Strip last column u = D\F; % solve the system. u = [u;gn]; % err(i) = norm(u-uexact(x),Inf); end figure loglog(h,err,'-o') % Plot the error in logscale xlabel('h'); ylabel('Error')
Number 3
Please do it yourself. Ask me if you got stucked.