Supplemental Codes for Lecture 10.
Alfa Heryudono MTH572/472 Numerical PDE
Our goal is to solve several simple PDEs in 1D using method of lines. In particular, we will discretize space with finite difference and advance the resulting system of ODEs in time with simple ODE solver. We will also check the accuracy and stability of the problem.
Contents
1-D Diffusion Equation with extra term.
Suppose we are trying to numerically simulate the following 1-D Diffusion equation in the domain ![$[-1,1]$](matlablecture10_5html_eq01893875229900969577.png) from time
from time  until time
until time 
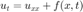
with boundary condition at 
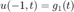
with boundary condition at 

and initial condition
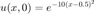
We want to solve it with 3-point stencil finite-difference in space and Forward Euler in time.
- Define sigma
 is ratio
is ratio 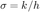 Hence we define
Hence we define  and
and  in the beginning of the program and the time step k will be computed by
in the beginning of the program and the time step k will be computed by  from there.
from there.
close all; clear all; sigma = 1e-2;
- Get 2nd-derivative Differentiation Matrix
n = 50; % Number of points a = -1; b = 1; h = (b-a)/(n-1); % Note that n points means n-1 intervals x = linspace(a,b,n).'; % Discretize the domain with n points. one = ones(n,1); % create a column vector of size n by 1 of ones D2 = spdiags([one -2*one one],[-1 0 1],n,n); D2(1,1:4) = [2 -5 4 -1]; D2(end,end-3:end) = [-1 4 -5 2]; % Modify first and last row (one-sided weights) D2 = (1/h^2)*D2; % Don't forget the 1/(h^2) factor
To accomodate the boundary conditions, strip the first and the last rows and separate the first and last columns from the main matrix
D2([1 end],:)=[]; LFCols = D2(:,[1 end]); D2(:,[1 end]) = [];
Plot the the eigenvalues scaled with time-step k of the modified differentiation matrix.
k = h*sigma; % time-step evscaled = k*eig(full(D2)); figure; z = exp(1i*pi*(0:200)/100); r = z - 1; s = 1; R = r./s; plot(R); fill(real(R),imag(R),'y'); hold on plot(real(evscaled),imag(evscaled),'*r') text(-1.25,0.3,'Stable Region'); xlabel('x'); ylabel('y') axis([-2.5 0.5 -1.5 1.5]), axis square, grid on
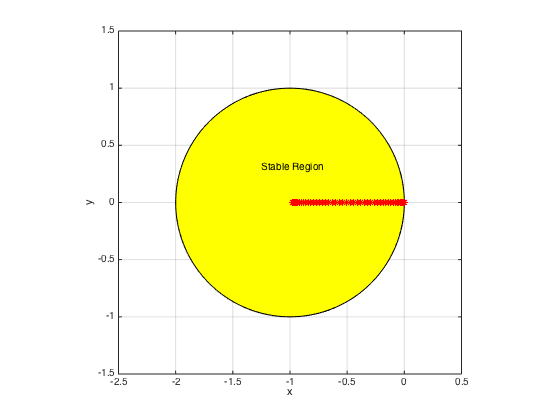
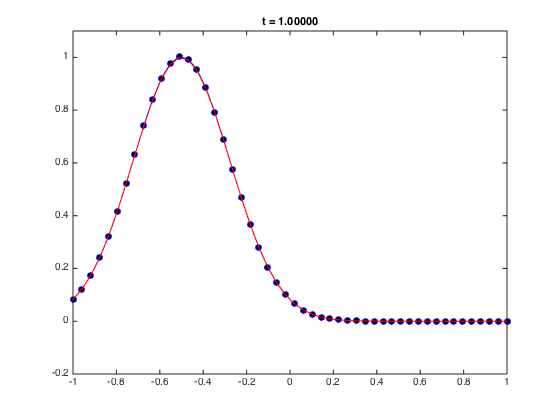
Note that the scaled eigenvalues are in the stability region. Hence, we expect this simulation to be stable. Now let's march the solution in time with Forward Euler.
uexact = @(x,t) exp(-10*((x+t)-0.5).^2); g1 = @(t) exp(-10*((a+t)-0.5)^2); % Left BC gn = @(t) exp(-10*((b+t)-0.5)^2); % Right BC f = @(x,t) -10.*(7+40*t^2-38*x+40.*x.^2+t.*(-38+80*x)).*exp(-10*((x+t)-0.5).^2); Tinit = 0; Tfinal = 1; t = Tinit; I = speye(n-2); u0 = uexact(x,t); % Initial condition u = u0; u(1) = g1(Tinit); u(end) = gn(Tinit); % Pre-allocate memory to store solution. figure graph1 = plot(x,u0,'-ob','markerfacecolor','k'); % Plot of numerical solution hold on graph2 = plot(x,u0,'-r'); % Plot of exact solution t1 = title(sprintf('t = %3.5f',t)); ylim([-0.2 1.1]) while t < Tfinal u(2:end-1) = (I + k*D2)*u0(2:end-1) + k*LFCols*[g1(t);gn(t)] + k*f(x(2:end-1),t); t = t + k; u(1) = g1(t); u(end) = gn(t); % Update time and boundary values. set(graph1,'ydata',u); % update the plot set(graph2,'ydata',uexact(x,t)); % update the plot set(t1,'String',sprintf('t = %3.5f',t)); pause(0.01) drawnow; % draw the updated plot immediately. u0 = u; end
1-D Advection Equation.
Suppose we are trying to numerically simulate the following 1D advection equation in the domain ![$[-1,1]$](matlablecture10_5html_eq01893875229900969577.png) from time
from time  until time
until time 
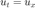
with boundary condition
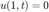
and initial condition
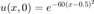
We want to solve it with 3-point stencil finite-difference in space and Backward Euler in time.
- Define sigma
 is ratio
is ratio 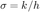 Hence we define
Hence we define  and
and  in the beginning of the program and the time step
in the beginning of the program and the time step  will be computed by
will be computed by  from there.
from there.
close all; clear all; sigma = 1;
- Get Differentiation Matrix
n = 500; % Number of points a = -1; b = 1; h = (b-a)/(n-1); % Note that n points means n-1 intervals x = linspace(a,b,n).'; % Discretize the domain with n points. one = ones(n,1); % create a column vector of size n by 1 of ones D = spdiags([-one one],[-1 1],n,n); D(1,1:3) = [-3 4 -1]; D(end,end-2:end) = [1 -4 3]; % Modify first and last row (one-sided weights) D = (0.5/h)*D; % Don't forget the 1/(2*h) factor
Since 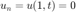 , then the last row and the last columns of D have to be removed (Strip Rows and Columns Method).
, then the last row and the last columns of D have to be removed (Strip Rows and Columns Method).
D(end,:)=[]; D(:,end)=[];
Plot the the eigenvalues scaled with time-step k of the modified differentiation matrix.
k = h*sigma; % time-step evscaled = k*eig(full(D)); figure; plot(real(evscaled),imag(evscaled),'*r'); hold on z = exp(1i*pi*(0:200)/100); r = z-1; s = z; R = r./s; plot(R); fill(real(R),imag(R),'y') text(0.5,0,'Unstable Region'); xlabel('x'); ylabel('y') axis([-2.5 2.5 -2 2]), axis square, grid on
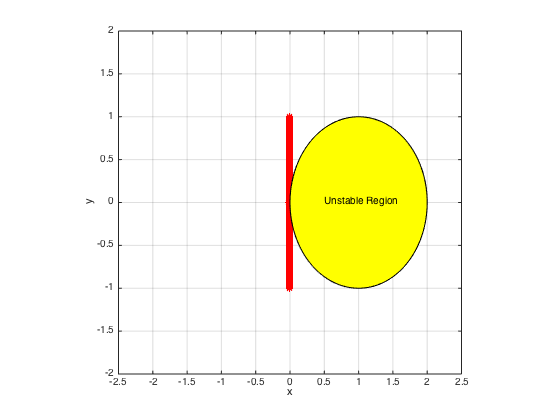
Note that the scaled eigenvalues are always in the stability region. Hence, we expect this simulation to be stable. Now let's march the solution in time with Backward Euler.
uexact = @(x,t) exp(-60*((x+t)-0.5).^2); Tinit = 0; Tfinal = 1; t = Tinit; I = speye(n-1); u0 = uexact(x,t); % Initial condition u = u0; u(end) = 0; % Pre-allocate memory to store solution. figure g1 = plot(x,u0,'-ob','markerfacecolor','k'); % Plot of numerical solution hold on g2 = plot(x,u0,'-r'); % Plot of exact solution t1 = title(sprintf('t = %3.5f',t)); ylim([-0.2 1.1]) while t < Tfinal t = t + k; u(1:end-1) = (I-k*D)\u0(1:end-1); set(g1,'ydata',u); % update the plot set(g2,'ydata',uexact(x,t)); % update the plot set(t1,'String',sprintf('t = %3.5f',t)); pause(0.01) drawnow; % draw the updated plot immediately. u0 = u; end
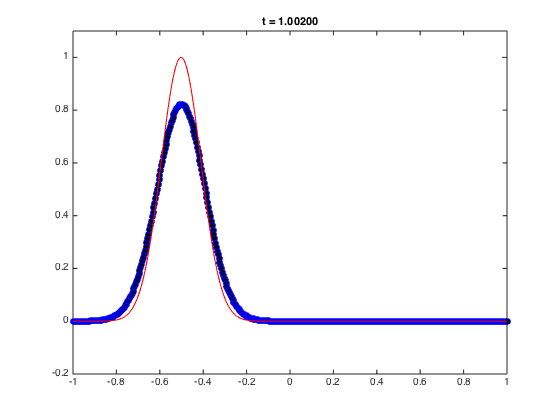
We will discuss why there is a dissipation phenomena in the Advection case.