An axes Style window will be displayed.

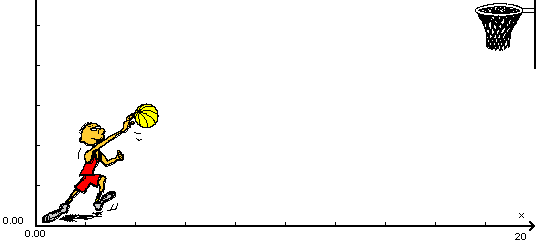
The Graph window is resized and the entire "basketball" picture is now visible.
An axes Style window will be displayed.

The Graph window is resized and the entire "basketball" picture is now visible.

|
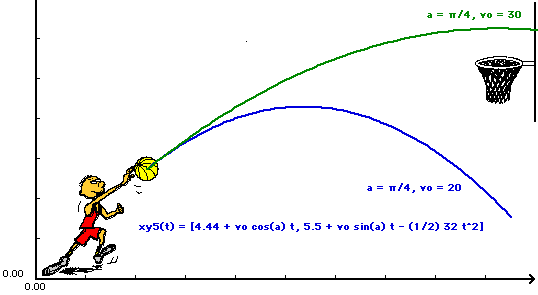
x(t) = x0 + v0 cos(a) t |
|
y(t) = y0 + v0 sin(a) t - (1/2) g t^2 |
|
(x0, y0) = coordinates of the initial position of the ball just before it is thrown (ft) v0 = velocity with which the ball is thrown (ft/sec) a = the angle with the horizontal at which the ball is thrown (radians) g = acceleration due to gravity = 32 ft/sec^2 |
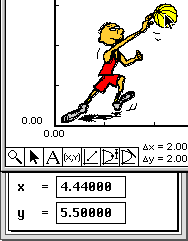
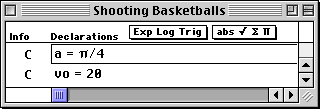
The template xy#(t) = [ , ] is written into the first cell in the Work window.
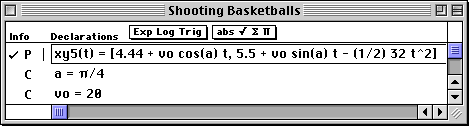
xy#(t) = [x0 + v0 cos(a) t, y0 + v0 sin(a) t - (1/2) g t^2]
(with numbers in place of x0, y0, and g).

|
Copyright 2000-2008 Adam O. Hausknecht and Robert E. Kowalczyk