Predator-Prey Models

A typical predator-prey problem can be modeled by a system of differential equations. For example, consider the following system of differential equations

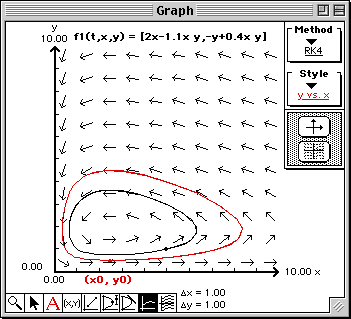
dx/dt = 2x - 1.1xy, dy/dt = -y + 0.4xy

where

x = population of pest insects
y = population of predator insects

Suppose that at t = 0, there are five times more pest insects than predator insects. The pests are becoming a real annoying problem to the local human population. Should you spray with insecticides knowing that both pest and predators will be destroyed?

Let's use TEMATH's numerical System of Differential Equations Solver to investigate this problem from a graphical point of view.

TEMATH is already in System Diff Eq. plot mode and the system of differential equations has been entered into the Work window. Thus, we are all set up to analyze the pest insect problem.

Click the Axes button in the upper right corner of the Graph window.
The x-axis and y-axis will be drawn.

We now need to enter the initial conditions. We are given that there are five times more pest insects than predator insects. Thus, we will let x(0) = 5 and y(0) = 1. To enter these initial conditions into TEMATH,

Click in the Domain & Range window to make it active.
Enter 0 into the "t =" cell, enter 5 into the "x =" cell, and enter 1 into the "y =" cell.
Click the enter button or press the Enter key.
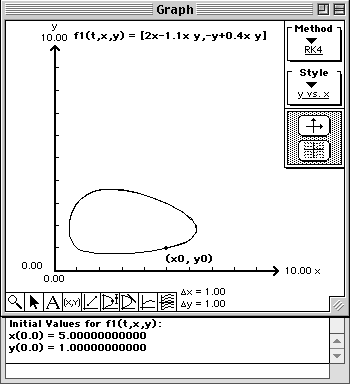
The solution curve to the system of differential equations will be drawn in the phase plane in the Graph window. Note that the initial conditions are represented by the dot on the solution curve.

To get a sense of the direction of movement along the solution curve as a function of time t,

Click the "Direction Field" button in the Graph window.

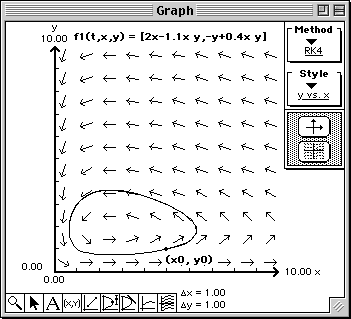
Direction field plot

Describe the pest and predator populations as a function of time.

Now we need to determine what happens to the insect populations if we decide to spray insecticide to "control" the pest insect population. It is given that the insecticide will kill both the pest and predator insects. Let's assume that spraying the insecticide will kill 50% of both insect populations.

Click in the Work window to make it active.
Click the vertical line between "S" and "f1".
The line should change its color to red and the next solution curve will be plotted using the color red.
Click in the Domain & Range window to make it active.
Enter 2.5 into the "x =" cell, and enter 0.5 into the "y =" cell. (Insect populations have been reduced by 50%)
Click the enter button or press the Enter key.
The solution curve to the system of differential equations will be drawn in the phase plane in the Graph window.

Did spraying the insecticide solve the pest insect problem?

To get a better visual representation of the pest insect population,

Position the arrow cursor over the Style pop-up menu in the Graph window.
Press the mouse button and select the "x vs. t" plot style.

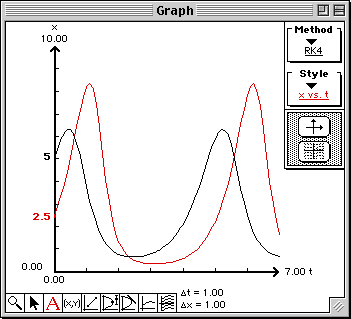
The size of the population of pest insects is plotted as a function of time.

You can clearly see from this graph that the pest insect population will grow even larger after spraying with the insecticide. Why do you think this is true?

What do you think would happen if you used an even stronger insecticide, say, one that kills 80% of both insect populations?

Return to Topic Start

Return to Examples Menu