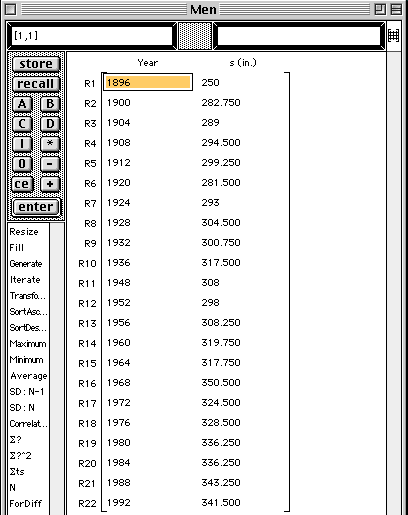
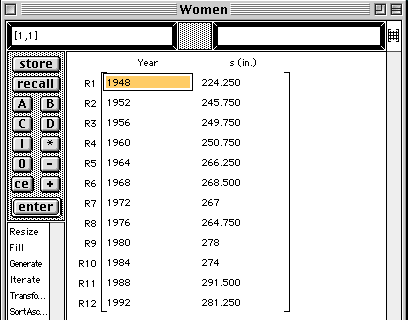
The data will be displayed. The distances are measured in inches.
|
Caution: TEMATH's tools will occasionally write results
into this Report window. The results will be written on the last line in the window.
When this happens, you will need to scroll back to your position in the instructions.
You may want to print a copy of the instructions in this Report window before you begin. |
The data will be displayed. The distances are measured in inches.


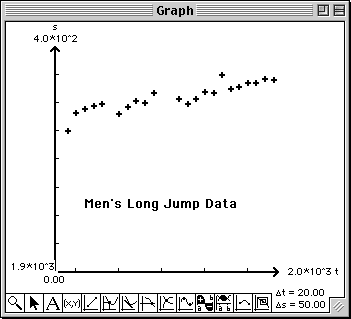
Carefully examine the plot of the data. Note that there are breaks in the data for the years 1912 to 1920 and 1936 to 1948. What happened in these years? Also, note the stellar performance by Bob Beamon in the 1968 Olympics in the mile high city of Mexico City.
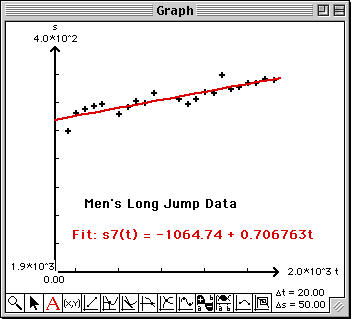
The least squares line will be drawn in the Graph window and its equation will be written into the first row of the Work window.
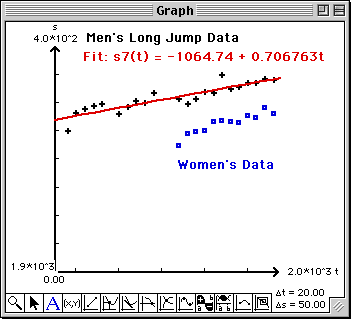
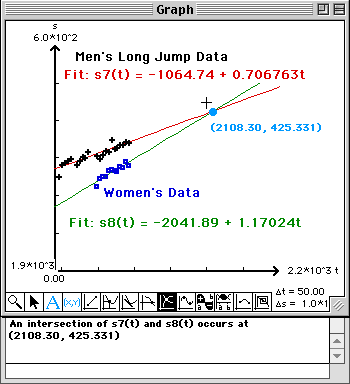
Examine the plot of the Women's data and compare it to the men's data.
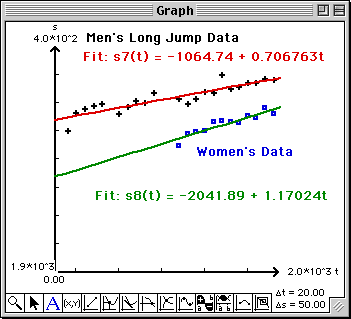
The least squares line will be drawn in the Graph window and its equation will be written into the first row of the Work window.
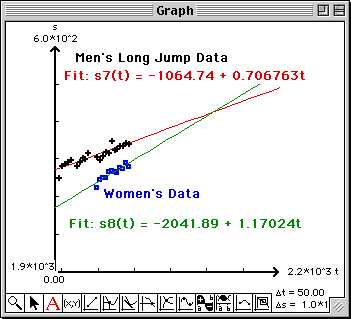
The coordinates of the point of intersection will be written into this Report window at the bottom.
|
Copyright 2000-2008 Adam O. Hausknecht and Robert E. Kowalczyk