Newton's Method for Approximating the Root (Zero) of a Function

Caution: TEMATH's tools will write the values of computed results at the bottom of this Report window. This will cause you to constantly scroll between the computed results and the instructions for this activity. You may want to print a copy of the contents of the Report window before you begin this activity.

Newton's Method is defined by the iteration procedure

x[n+1] = x[n] - f(x[n])/f'(x[n]), n = 0, 1, 2, 3, ...

Using Newton's Method to Find the Square Root of a Number

The positive root of the function f(x) = x^2-2 is

2. Let's use Newton's method to find this root.

Plot y1(x) = x^2-2 on -5x5.
Click the Single Root Finder tool on the Tool Palette.
Select Newton from the Method pop-up menu in the Graph window.
Enter the initial approximation x0 = 5 by clicking in the Graph window at x = 5. You can also enter the initial value through the Domain & Range window by typing 5 into the "x =" cell and pressing the Enter key.

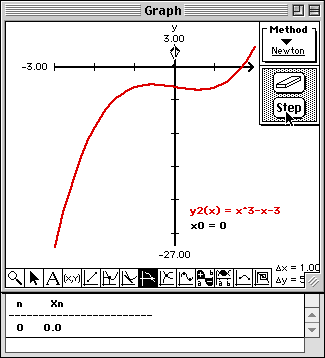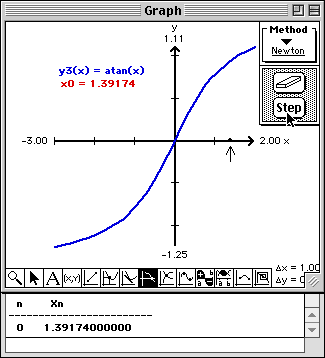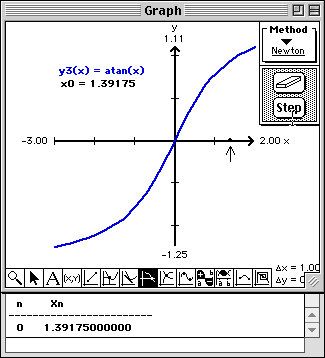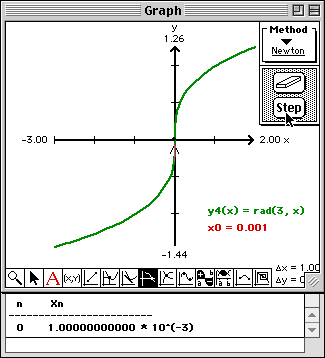
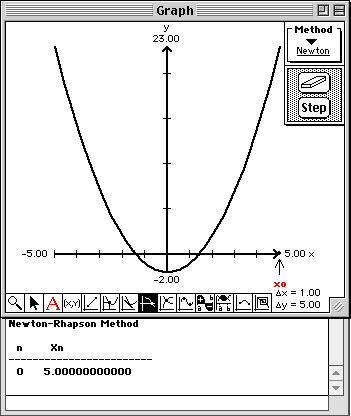
Note that a point is drawn on the x-axis at the initial approximation, a arrow is drawn pointing to the current approximation, and the value of the current approximation is written into this Report window.
Click the "Step" button to perform one iteration of Newton's Method.

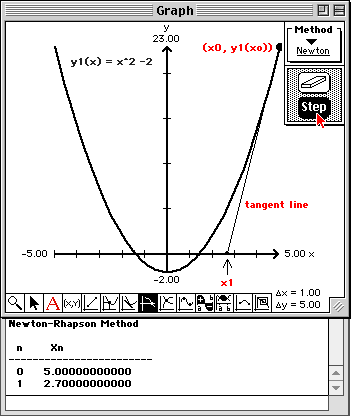
Note that the tangent to the curve at the initial approximation is drawn, and a point and arrow is drawn at the next approximation. Also, the value of the new approximation is written into this Report window.
Continue to click the "Step" button.

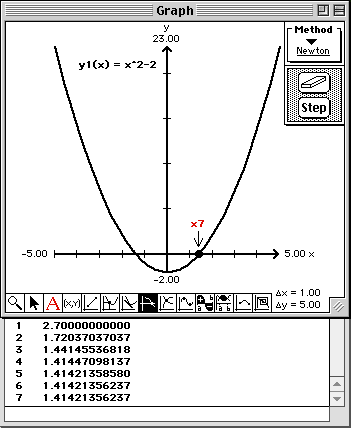
Observe the convergence of Newton's Method from a visual point of view in the Graph window and from a numerical point of view in the Report window.

How many iterations did it take to get 12 digit accuracy? Note that as the iterates get close to the root, the number of significant digits in the approximation doubles at each step.

Some of the Pitfalls of Newton's Method

1. Cycling

Plot y2(x) = x^3-x-3 on -3x2.
If the Single Root Finder tool on the Tool Palette is not selected, click it to select it.
Click in the Domain & Range window, type 0 into the "x =" cell, and press the Enter Key. This enters the initial approximation x0 = 0.
Continue to click the Step button and watch the cycling behavior of the approximations.

In this case, Newton's Method does not converge to the root using the initial approximation x0 = 0.

2. Dependency on the value of the initial approximation.

Plot y3(x) = atan(x) on -3x2.
If the Single Root Finder tool on the Tool Palette is not selected, click it to select it.
Click in the Domain & Range window, type 1.39174 into the "x =" cell (or simply copy 1.39174 and paste it into the Domain & Range window), and press the Enter Key. This enters the initial approximation x0 = 1.39174.
Continue to click the Step button.

Note that it appears that Newton's Method is caught in a cycling mode. Be persistent and click at least 17 steps. Note that Newton's Method finally converges to the root at 0.

What happens if we change the value of the initial approximation by one unit in the fifth decimal place, that is, what will happen if we use the initial approximation x0 = 1.39175?

Plot y3(x) = atan(x) on -3x2. This will clear the Graph window of the previous iterations.
Click in the Domain & Range window, type 1.39175 into the "x =" cell, and press the Enter Key.

Continue to click the Step button.

Note that it appears that Newton's Method is caught in a cycling mode. Be persistent and click at least 17 steps. Note that Newton's Method diverges.

3. Divergence

Plot y4(x) = rad(3, x) on -3x2. rad(3, x) is TEMATH's notation for the cube root x^(1/3).
If the Single Root Finder tool on the Tool Palette is not selected, click it to select it.
We know that there is a root at x = 0. Let's use an initial approximation very, very close to the root.
Click in the Domain & Range window, type 0.001 into the "x =" cell, and press the Enter Key.
Continue to click the Step button.

Note that in this case, no matter how close your initial approximation is to the root, Newton's Method will diverge. Why does this happen?

Return to Topic Start

Return to Examples Menu