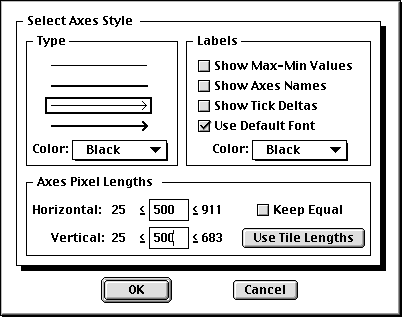
|
Caution: TEMATH's tools will write the values of
computed results at the bottom of this Report window. This will cause you to constantly
scroll between the computed results and the instructions for this activity. You may want
to print a copy of the contents of the Report window before you begin this activity. |

|
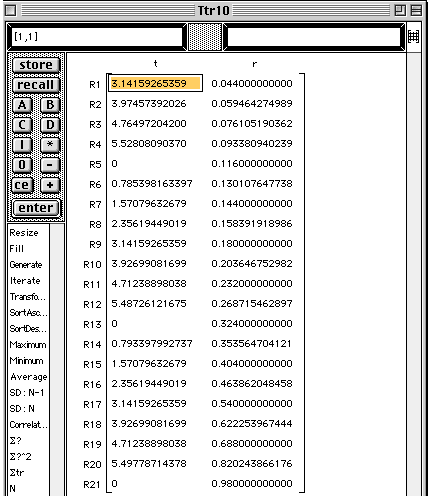
bt r = a e |
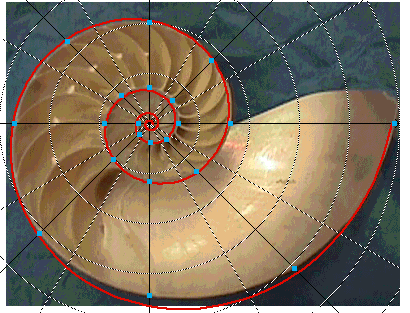
The points that we sampled along the spiral of the Nautilus shell are plotted on top of the picture of the shell.
The "Least Squares" logarithmic spiral fit is plotted on top of the picture of the shell. Note how well you can mathematically model nature.

![]()

The coordinates of the points drawn in the Graph window will be stored in a data table written into the top cell of the Work window.
The Data Table window is opened and the data is displayed.
The cursor changes to a downward-pointing arrow.
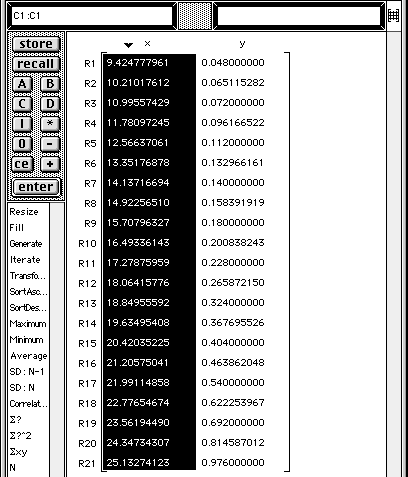
The values of the data are pasted into the table.
The cursor changes to a downward-pointing arrow.
The fill function template "x(i) = ?" is displayed in the command area.
|
3 |

The first column is filled with the angles that we need.
The data table will be added to the Work window.
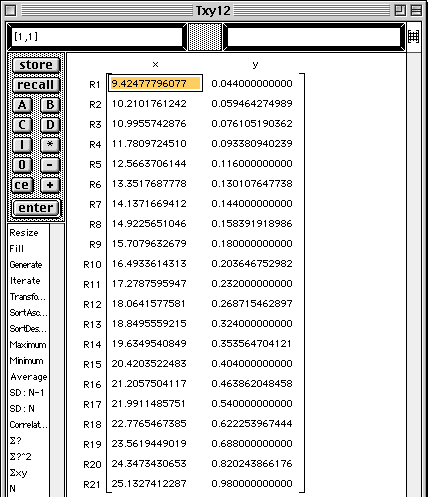
The least squares natural exponential fit is drawn in the Graph window and its algebraic expression is written into the top cell of the Work window.

The expression for the least squares natural exponential fit is pasted into the top cell of the Work window.
Your fit along with the picture of the shell is drawn in the Graph window.
|
Copyright 2000-2008 Adam O. Hausknecht and Robert E. Kowalczyk