The Mean Value Theorem

Caution: In this activity, TEMATH's icon tools will write computed results into this Report window below the instructions. This will cause you to constantly scroll between the computed results and the instructions for this activity. You may want to print a copy of the contents of the Report window before you begin.

Many times when we use a theorem in solving a problem, we take for granted that the hypotheses given in the theorem are satisfied and we never check to see if that is in fact true. We simply assume that the result of the theorem will be true. In this lab, we will thoroughly investigate the importance of the hypotheses of a theorem and try to convince ourselves that before we solve a problem by applying a theorem, we should verify that the hypotheses given in the theorem are satisfied. The mean value theorem will be used as the basis for all our explorations in this lab.

The Mean Value Theorem
Let f be a function that satisfies the following hypotheses:

1. f is continuous on the closed interval [a, b].
2. f is differentiable on the open interval (a, b).

Then there is a number c in (a, b) such that

f'(c) = (f(b) - f(a))/(b - a)

The mean value theorem states that under the specified hypotheses, there is a point in the interval of interest such that the slope of the tangent line at that point is equal to the slope of the secant line connecting the two endpoints of the graph of the function. In other words, the average rate of change of the function f on the interval [a, b] is equal to the instantaneous rate of change of the function f at some point c in (a, b).

Approximating the Value of c

In this exploration, we will graphically find an approximation to the value of c for which the mean value theorem is satisfied. Let's use the function y1(x) = 2x-x^2 which satisfies both of the hypotheses of the Mean Value Theorem on the interval [0, 3].

Plot y1(x) = 2x-x^2 on 0x3.

Next, we need to draw the secant line and find its slope. To do this,

Click the Line Segment tool on the Tool Palette in the Graph window.
Move the "+" cursor to the left endpoint of the curve, click and hold down the mouse button, drag the mouse to the right endpoint of the curve, and release the mouse button.
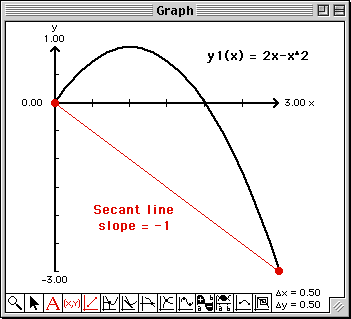
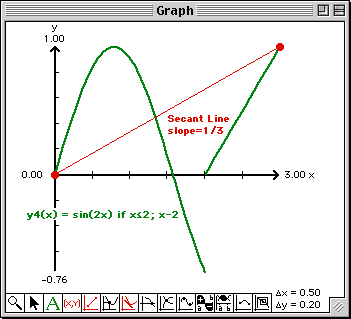
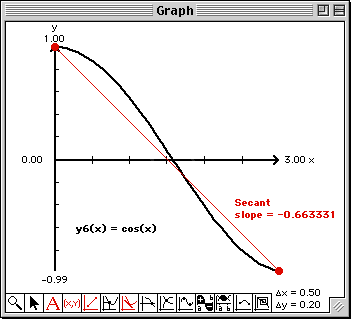
The secant line will be drawn and the slope of the secant line will be written into this Report window at the bottom. Note that the slope of the secant line is -1.

You can also draw the line by using the Domain & Range window. For example, to draw this same line, you would do the following:

Enter the coordinates (0, 0) of the left endpoint of the curve into the "x1 =" and "y1 =" cells.
Click the Enter button.
Enter the coordinates (3, -3) of the right endpoint of the curve into the "x2 =" and "y2 =" cells.
Click the Enter button.
This is the preferred method when you want to enter the endpoints of the line exactly.

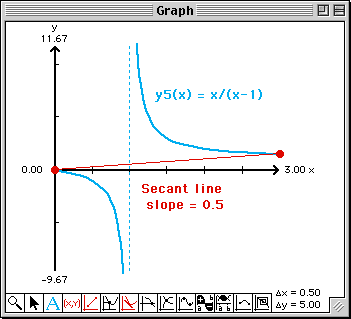
Note: If f(x) is a function in the Work window, you can enter the end points for a line as (0, f(0)) and (3, f(3)) in the cells in the Domain & Range window. TEMATH will replace f(0) and f(3) with their values.

Plot of y1 with secant line

To find the value of c given in the Mean Value Theorem, we need to find a tangent line to the curve that has the same slope as the secant line. Examine the curve in the Graph window and try to visualize a point where the tangent to the curve will be parallel (same slope) to the secant line. When you have visualized this point, draw the tangent line at that point by doing the following:

Click the Tangent Line tool on the Tool Palette in the Graph window.
Click in the upper part of the Tangent Line tool's icon to display its pop-up menu. Select the picture of the "long, thick line" option.
Click the point on the curve where you want the tangent line drawn.
Note that the slope of the tangent line is written into this Report window.
If the slope of the tangent line is not approximately equal to the slope of the secant line, click at other points on the curve to draw additional tangent lines until you find one with approximately the same slope as the secant line.
If the graph gets messy with too many tangent lines, select Delete All Tangents from the Edit menu to erase all the tangent lines from the Graph window.
Note: You can also enter the x-value of the point where you want the tangent line drawn by entering its value into the "x =" cell of the Domain & Range window and by clicking the Enter button or pressing the Enter key. In this way, you can enter the x-value more accurately.

What is an approximate value of c? Find the exact value of c by using some algebra.

Differentiability and the Mean Value Theorem

Are both the continuity and differentiability hypotheses really necessary for the result of the Mean Value Theorem to be always true? What happens if we violate one of these hypotheses, for example, what if we pick a function that is not differentiable on the open interval (a, b). To find out what happens, let's examine the function f(x) = ( (x-1)^2 )^(1/3) on the closed interval [0, 3].

Why is f(x) not differentiable on (0, 3)?

Plot y2(x) = rad(3, (x-1)^2) on 0x3.
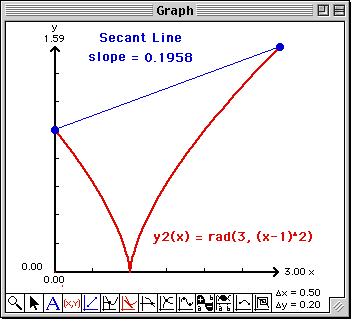
In TEMATH, the cube root function is entered as rad(3, (x - 1)^2). Note that rad(n, g(x)) is TEMATH’s predefined function for the nth root of g(x).
Use the Line Segment tool to draw the secant line connecting the endpoints of the graph.
If possible, use the Tangent Line tool to "try" drawing a tangent line to the curve that has the same slope as the secant line.

Is it possible to draw a tangent line that is parallel to the secant line? Can you find a number c that satisfies the Mean Value Theorem? If the differentiability hypothesis is violated, can we guarantee that a c will exist that satisfies the result of the Mean Value Theorem?

Continuity and the Mean Value Theorem

In this exploration, we will investigate to see what happens if we violate the continuity hypothesis for f(x) on the closed interval [a, b]? Let's examine the piecewise function f(x) = x if x

3; 2 otherwise on the closed interval [0, 3].

Why is f(x) not continuous on [0, 3]?

Plot y3(x) = x if x3;2 on 0x3.
Use the Line Segment tool to draw the secant line connecting the endpoints of the graph.
Be careful! The coordinates of the endpoints of the graph are (0, 0) and (3, 2).
If possible, use the Tangent Line tool to "try" drawing a tangent line to the curve that has the same slope as the secant line.

Is it possible to draw a tangent line that is parallel to the secant line? Can you find a number c that satisfies the Mean Value Theorem? If the continuity hypothesis is violated, can we guarantee that a c will exist that satisfies the result of the Mean Value Theorem?

Mean Value Theorem Problems

Plot y4(x) = sin(2x) if x2; x-2 on 0x3.
Use the Line Segment tool to draw the secant line connecting the endpoints of the graph.
If possible, use the Tangent Line tool to draw a tangent line to the curve that has the same slope as the secant line.

Is y4(x) continuous on [0, 3]? Is y4(x) differentiable on (0, 3)?
Can you draw a tangent line that is parallel to the secant line?
Is it possible for one or both of the hypotheses of the mean value theorem not to be satisfied but the results of the mean value theorem still be true?

Plot y5(x) = x/(x-1) on 0x3.
Use the Line Segment tool to draw the secant line connecting the endpoints of the graph.
If possible, use the Tangent Line tool to draw a tangent line to the curve that has the same slope as the secant line.

Is y5(x) continuous on [0, 3]? Is y5(x) differentiable on (0, 3)? Can you draw a tangent line that is parallel to the secant line?

From these examples, we can conclude that if the hypotheses of the Mean Value Theorem are violated, then the result of the Mean Value Theorem is not guaranteed.

Finding More Than One Value of c

Plot y6(x) = cos(x) on 0x3.
Use the Line Segment tool to draw the secant line connecting the endpoints of the graph.
If possible, use the Tangent Line tool to draw all tangent lines to the curve that have the same slope as the secant line.

Can there be more than one value of c that satisfies the mean value theorem?

Return to Topic Start

Return to Examples Menu