Linear Systems of Differential Equations

Caution: TEMATH's tools will write informational prompts at the bottom of this Report window. This will cause you to scroll between the prompts and the instructions for this activity. You may want to print a copy of the contents of the Report window before you begin this activity.

TEMATH's System of Differential Equations Solver can be used to numerically and qualitatively analyze a system of two differential equations in two unknowns. To use TEMATH's System of Differential Equations Solver,

Select System Diff Eq from the Graph menu.

Linear Systems of Differential Equations with Real Eigenvalues

Example 1: One positive and one negative eigenvalue; Equilibrium point is a saddle point.

dx/dt = 3x + 2y

dy/dt = 4x + y

The eigenvalues are -1 and 5. The eigenvectors are (1, -2) and (1, 1).

Select f1(t,x,y) = [3x+2y,4x+y] in the Work window.
Click the Axes button in the Graph window to plot the axes.
Click the Direction Field button in the Graph window. The direction field will be plotted.
Select xy1(t) = [t,-2t] in the Work window. xy1(t) = [t,-2t] are the parametric equations for the straight line solution corresponding to the eigenvector V1 = (1, -2).
Select Overlay Plot from the Graph menu.
Select xy2(t) = [t,t] in the Work window. xy2(t) = [t,t] are the parametric equations for the straight line solution corresponding to the eigenvector V2 = (1, 1).
Select Overlay Plot from the Graph menu.
Select f1(t,x,y) = [3x+2y,4x+y] in the Work window. The System Solution Curve tool icon on the tool palette becomes highlighted. This tool allows you to draw solution curves in the Graph window. If the System Solution Curve tool icon is not highlighted, click the tool's icon to select it.
Click in the Graph window to enter the initial values and to draw the corresponding solution curve.
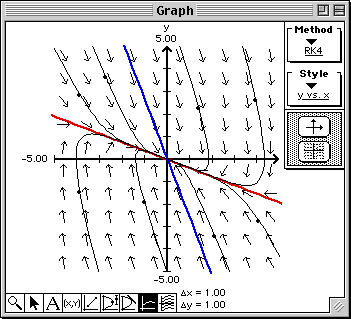
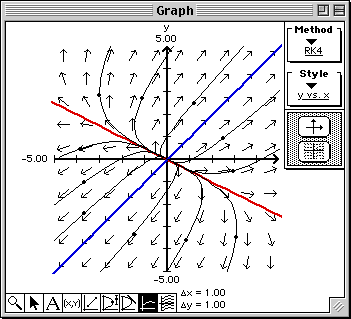
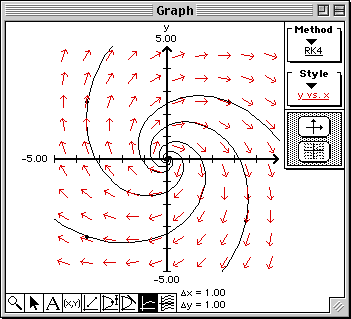
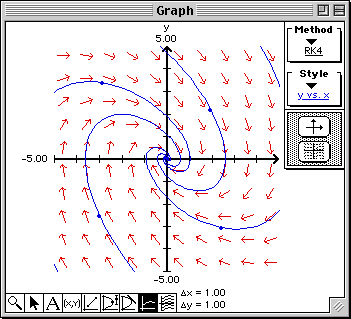
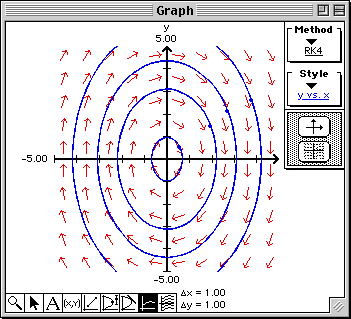
The initial values are the values of the x- and y-coordinates of the point you clicked with the initial time given in the "t =" cell of the Domain & Range window, for example, possible initial values are x(0) = 1 and y(0) = 2.
Click enough solution curves in the Graph window to give a picture of the general solution to the system of differential equations.

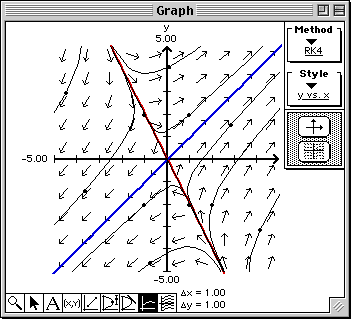
Note that the solution curves come in along the straight line solution xy1(t) = [t,-2t] (red line) and leave along the other straight line solution xy2(t) = [t,t] (blue line). Additionally, the equilibrium point at the origin is a saddle point.

Note: You can not plot an object in the Work window unless it has a checkmark to its left. If the object does not have a checkmark, click in the position where the checkmark should be and one will be drawn. At most, five objects can have checkmarks at the same time.

Example 2: Two negative eigenvalues; Equilibrium point is a sink.

dx/dt = y

dy/dt = -x - 3y

The eigenvalues are (-3+

(5))/2 and (-3-

(5))/2. The eigenvectors are (1, (-3+

(5))/2) and (1, (-3-

(5))/2).

Select f2(t,x,y) = [y,-x-3y] in the Work window.
Click the Axes button in the Graph window to clear the Graph window and to plot the axes.
Click the Direction Field button in the Graph window.
Select xy3(t) = [t,(-3+sqrt(5))/2t] in the Work window.
Select Overlay Plot from the Graph menu.
Select xy4(t) = [t,(-3-sqrt(5))/2t] in the Work window.

Reminder: Click to the left of the P to display a checkmark and make the object active.
Select Overlay Plot from the Graph menu.
Select f2(t,x,y) = [y,-x-3y] in the Work window.
Click enough solution curves in the Graph window to give a picture of the general solution to the system of differential equations.

Note that the solution curves head toward the origin along the straight line solution xy3(t) = [t,(-3+sqrt(5))/2t] (red line). The equilibrium point at the origin is a sink.

Example 3: Two positive eigenvalues; Equilibrium point is a source.

dx/dt = 2x + 2y

dy/dt = x + 3y

The eigenvalues are 1 and 4. The eigenvectors are (-2, 1) and (1, 1).

Select f3(t,x,y) = [2x+2y,x+3y] in the Work window.
Click the Axes button in the Graph window to clear the Graph window and to plot the axes.
Click the Direction Field button in the Graph window.
Select xy5(t) = [-2t,t] in the Work window.
Select Overlay Plot from the Graph menu.
Select xy6(t) = [t,t] in the Work window.
Select Overlay Plot from the Graph menu.
Select f3(t,x,y) = [2x+2y,x+3y] in the Work window.
Click enough solution curves in the Graph window to give a picture of the general solution to the system of differential equations.

Note that the solution curves leave the origin along the straight line solution xy5(t) = [-2t,t] (red line). The equilibrium point at the origin is a source.

Linear Systems of Differential Equations with Complex Eigenvalues

Example 4: Complex eigenvalues with positive real part; Equilibrium point is a spiral source.

dx/dt = x + 2y

dy/dt = -2x + y

The eigenvalues are 1 ± 2i.

Select f4(t,x,y) = [x+2y,-2x+y] in the Work window.
Click the Axes button in the Graph window to clear the Graph window and to plot the axes.
Click the Direction Field button in the Graph window.
Click enough solution curves in the Graph window to give a picture of the general solution to the system of differential equations.

Note that all solution curves spiral out from the origin. The equilibrium point at the origin is a spiral source.

Example 5: Complex eigenvalues with negative real part; Equilibrium point is a spiral sink.

dx/dt = y

dy/dt = -x - y

The eigenvalues are -(1/2) ± (

(3)/2)i.

Select f5(t,x,y) = [y,-x-y] in the Work window.
Click the Axes button in the Graph window to clear the Graph window and to plot the axes.
Click the Direction Field button in the Graph window.
Click enough solution curves in the Graph window to give a picture of the general solution to the system of differential equations.

Note that all solution curves spiral in towards the origin. The equilibrium point at the origin is a spiral sink.

Example 6: Complex eigenvalues with zero real part; Equilibrium point is a center.

dx/dt = y

dy/dt = -2x

The eigenvalues are ±

(2)i.

Select f6(t,x,y) = [y,-2x] in the Work window.
Click the Axes button in the Graph window to clear the Graph window and to plot the axes.
Click the Direction Field button in the Graph window.
Click enough solution curves in the Graph window to give a picture of the general solution to the system of differential equations.

Note that all solution curves circle the origin along an elliptical path. The equilibrium point at the origin is a center.

Return to Topic Start

Return to Examples Menu