Linear Programming Problems

TEMATH has tools for solving linear programming problems using either the graphical method or the simplex method.

Caution: TEMATH's tools will write the values of computed results at the bottom of this Report window. This will cause you to constantly scroll between the computed results and the instructions for this activity. You may want to print a copy of the contents of the Report window before you begin this activity.

Using the Graphical Method to Solve a Linear Programming Problem

Example 1:

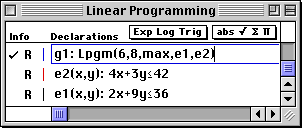
Maximize z = 6x + 8y subject to the constraints:

2x + 9y

36
4x + 3y

42
x

0, y

For this example, the constraints and objective function have already been entered into TEMATH. To enter a linear program, do the following:

To enter a constraint,

Select New Equation from the Work menu, enter the constraint into the Work window, and press the Enter key.

To enter and fill in a linear program template,

Select New Linear Pgm from the Tools menu.
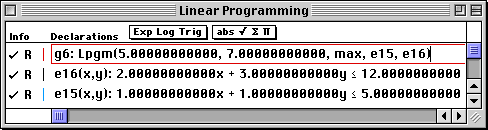
The template g#: Lpgm(a,b,max/min,ineqs) is written into the first cell of the Work window.
Replace a with the coefficient of x in the objective function,
Replace b with the coefficient of y in the objective function,
Replace max/min with max or min, and replace ineqs with the names of the equations representing the constraints.
Note: You do not have to enter the x0 and y0 constraints. TEMATH automatically includes them.

To analyze this linear programming problem, do the following:

If g1: Lpgm(6,8,max,e1,e2) is not selected in the Work window, then click on it to select it.
Select Plot from the Graph menu.

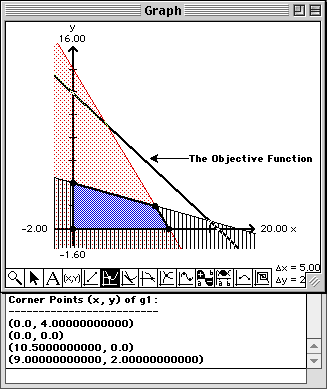
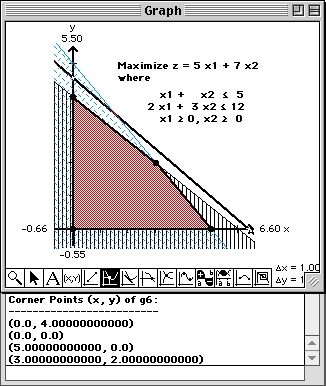
Note that the two inequality constraints are plotted, the region of feasible solutions is shaded, and circles are placed at the corner points. Additionally, the coordinates of the corner points are written at the bottom of this Report window.

Note that the Tracker tool icon

has been highlighted and that a black line is drawn in the Graph window representing the objective function for a particular value of z. To visualize where the objective function attains its maximum value,

Place the arrow cursor on the line representing the objective function, press and hold down the mouse button, and drag the line across the region of feasible solutions.
Notice that as you drag the line, the corresponding z-value is shown in the "z =" cell of the Domain & Range window.
Drag the line across the region of feasible solutions until you find the approximate point where the objective function attains its maximum value (you could also find the minimum value).

To find the maximum value more precisely,

Click in the Domain & Range window to make it the active window.
Click the Step button.

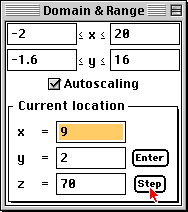
The line representing the objective function is moved to one of the corner points, the (x, y) coordinates of the corner point are written into the "x =" and "y =" cells of the Domain & Range window, and the value of the objective function z is written into the "z =" cell.
Continue to click the Step button until you have traversed all the corner points and found the maximum value of the objective function.

Example 2:

Minimize z = 150x + 120y subject to the constraints:

x + y

150
2x + y

200
x + y

60
x

10, y

Plot g2: Lpgm(150,120,min,e3,e4,e5,e6,e7).

Drag the objective function line to visualize where the minimum value will occur within the region of feasible solutions.

Find the exact minimum (and maximum) value of the objective function by using the Domain & Range window to traverse all the corner points.

Using the Simplex Method to Solve a Linear Programming Problem

Example 3:

Maximize z = 5 x1 + 7 x2 subject to the constraints:

x1 + x2

5
2 x1 + 3 x2

12
x1

0, x2

The matrix containing the constraints and the objective function is saved in the Work window as Example3[3,3].

Select Example3[3,3] in the Work window.
Select Show Matrix from the Work window.
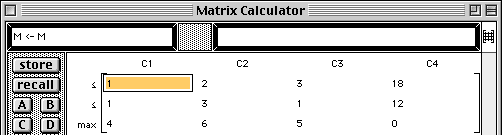
The Matrix Calculator window opens displaying the contents of the matrix. Note that the first two rows contain the coefficients of the constraints and the last row contains the coefficients of the objective function. Further note that the row labels contain the inequality symbols and the max or min for the objective function.
Click the store button and then click the A button.
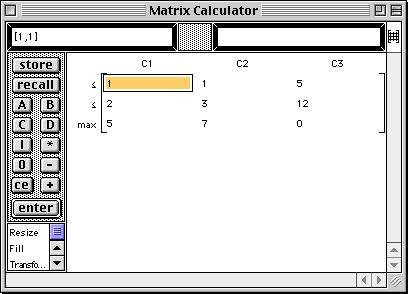
This will save a copy of the matrix in memory A for future (and backup) use.

To simply solve the linear programming problem,

Scroll the list of matrix commands (lower left corner of the Matrix Calculator window) until you find the LinProg command.
Double-click the LinProg command.
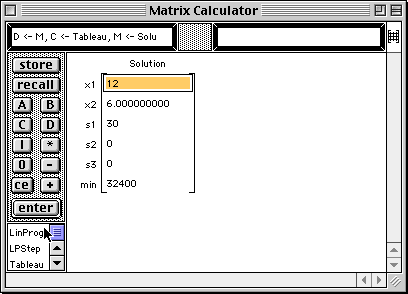
The solution to the linear programming problem is displayed in the Matrix Calculator window. The maximum value of z = 29 occurs at x1 = 3 and x2 = 2. Note that the values of slack variables are also given.

To find the Simplex Tableau and step through the Simplex method,

Click the recall button and then click the A button.
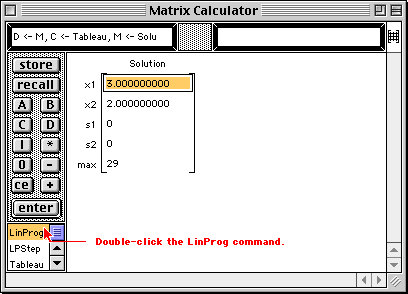
This places the original coefficient matrix back into the window.
Double-click the LPStep command in the matrix command list.
The initial Simplex Tableau is displayed in the Matrix Calculator window and the pivot element is highlighted.
Click the OK button.
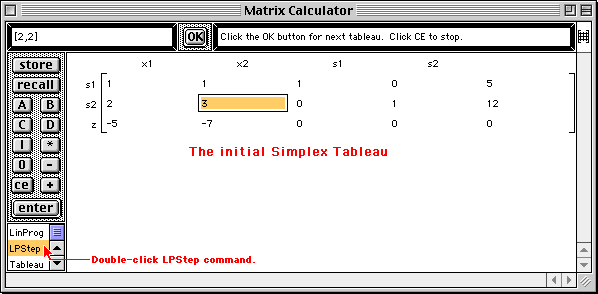
One step of the Simplex method is performed and the second tableau is displayed with the next pivot element highlighted.
Click the OK button.
The next (and last) step of the Simplex method is performed and the final tableau is displayed with the solution shown in the last column.

To graph this linear programming problem,

Click the recall button and then click the A button.
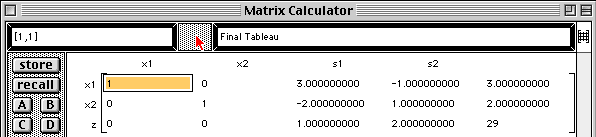
This places the original coefficient matrix back into the window.
Select Generate Linear Pgm from the Tools menu.
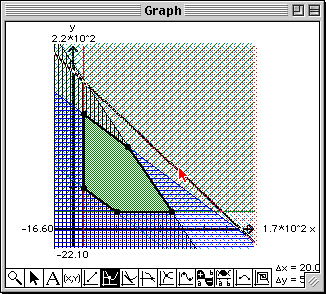
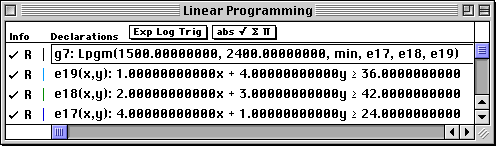
The constraints and objective function are entered into the Work window and the region of feasible solutions is plotted in the Graph window.

It is only possible to graphically solve linear programming problems in two variables.

Example 4 (Phase I - Phase II Method):

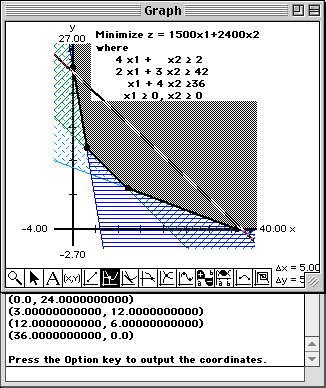
Minimize z = 1500 x1 + 2400 x2 subject to the constraints:

4 x1 + x2

24
2 x1 + 3 x2

42
x1 + 4 x2

36
x1

0, x2

The matrix containing the constraints and the objective function is saved in the Work window as Exampl4[4,3].

Select Exampl4[4,3] in the Work window.
Select Show Matrix from the Work menu.
Click the store button and then click the A button.
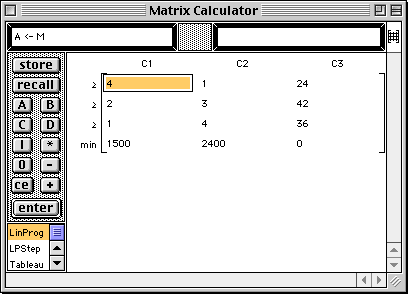
This will save a copy of the matrix in memory A for future (and backup) use.

To simply solve the linear programming problem,

Double-click the LinProg command.
The minimum value of z = 32,400 occurs at x1 = 12 and x2 = 6.

To find the Simplex Tableau and step through the Simplex method,

Click the recall button and then click the A button.
This places the original coefficient matrix back into the window.
Double-click the LPStep command in the matrix command list.
The initial Simplex Tableau for the Phase I - Phase II method is displayed.
Click the OK button.
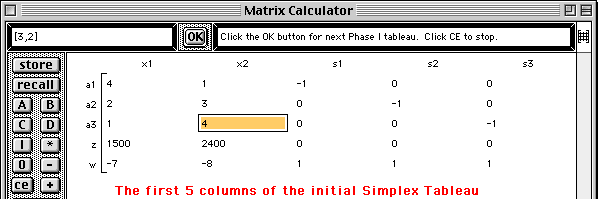
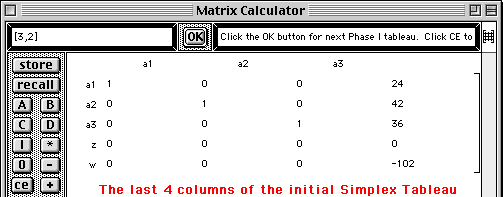
The first step of the Simplex method is performed and the second Phase I tableau is displayed with the next pivot element highlighted.
Click the OK button.
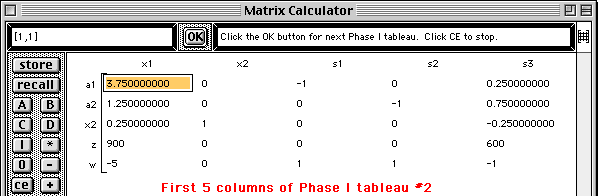
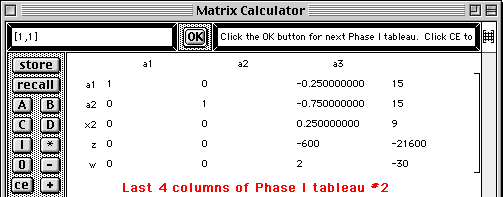
The second step of the Simplex method is performed and the third Phase I tableau is displayed with the next pivot element highlighted.
Click the OK button.
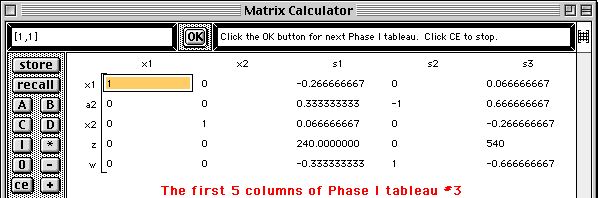
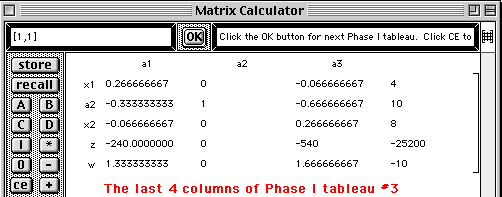
The third step of the Simplex method is performed and the first Phase II tableau is displayed with the next pivot element highlighted.
Click the OK button.
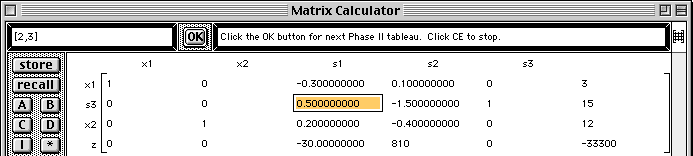
The last step of the Simplex method is performed and the final tableau is displayed with the solution shown in the last column.

To graph this linear programming problem,

Click the recall button and then click the A button.
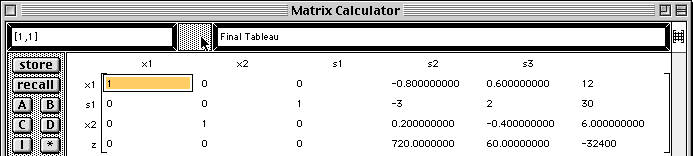
This places the original coefficient matrix back into the window.
Select Generate Linear Pgm from the Tools menu.
The constraints and objective function are entered into the Work window and the region of feasible solutions is plotted in the Graph window.

A Linear Programming Problem with Three Variables

Example 5:

Maximize z = 4 x1 + 6 x2 + 5 x3 subject to the constraints:

x1 + 2 x2 + 3 x3

18
x1 + 3 x2 + x3

12
x1

0, x2

0, x3

The matrix containing the constraints and the objective function is saved in the Work window as Exampl5[3,4].

Select Exampl5[3,4] in the Work window.
Select Show Matrix from the Work window.
Double-click the LinProg command.

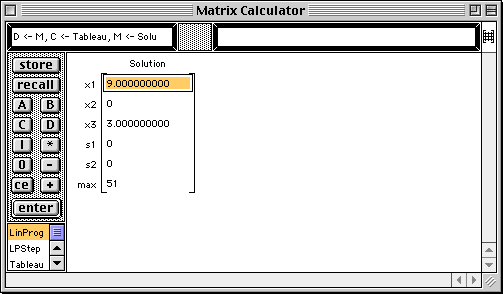
The maximum value of z = 51 occurs at x1 = 9, x2 = 0, and x3 = 3.

Practice Problems

Solve the following linear programming problem using the Graphical method.

Maximize z = 4x + 5y subject to the constraints:

x + y

10
2x + 3y

22
x

0, y

Select New Equation or Inequality from the Work menu.
Enter the first constraint x + y10 into the first cell of the Work window. Press the Option < keys to get the symbol . Note that you can also enter <= for .
Select New Equation or Inequality from the Work menu.
Enter the second constraint 2x + 3y22 into the first cell of the Work window.
Select New Linear Pgm from the Tools menu.

Fill in the template Lpgm(a,b,max/min,ineqs) located in the first cell of the Work window as Lpgm(4,5,max,e#,e##) where e# and e## are the names of the two constraints previously entered. Press the Enter key.

Select Plot from the Graph menu.

Solve this same linear programming problem using the Simplex method.

Select Calculators - Matrix Calculator... from the Work menu.
Double-click the Resize command located in the list of matrix commands.
Type 3,3 into the command area. Click the Enter button or press the Enter key.
Type 1 Enter 1 Enter 10 Enter to enter the coefficients of the first constraint. Enter means to press the Enter key instead of the return key.
Type 2 Enter 3 Enter 22 Enter to enter the coefficients of the second constraint.
Type 4 Enter 5 Enter 0 to enter the coefficients of the objective function.
Position the cursor to the left of the R1 row label. The cursor changes to a [. Click the mouse button to select the cell. Type . Press the Return key.
Typeinto the cell for the second row label. Press the Return key.
Type max into the cell for the third row label.
Click the store button and then click the A button.
This will save a copy of the matrix in memory A for backup use.
Double-click the LinProg command in the matrix command list.

Return to Topic Start

Return to Examples Menu