Approximate Integration and Area Under the Curve

The objectives of this activity are:

Use the integral to find the area under the curve.
Visualize the convergence of Riemann sums.
Investigate upper and lower estimates to the area under the curve.
Study the efficiency and rates of convergence for numerical integration techniques.

Caution: In this activity, TEMATH's Integration tool will write the values of areas into this Report window below the instructions. This will cause you to constantly scroll between the computed areas and the instructions. You may want to print a copy of the contents of the Report window before you begin this activity.

Do Riemann sums really converge to the value of the area under the curve?

Plot f(x) = x on 0x4 and 0y4

What is the area of the triangular region under the plotted line (use the formula for the area of a triangle)?

Click the Integration tool on the Tool Palette in the Graph window.
Select Left End Point from the Method pop-up menu in the Graph window.
Click the middle button (Draw button). Ten shaded rectangles will be drawn and the value of the total area of the rectangles will be written into the Report window.
Click the up arrow button.

Note that the number of rectangles doubles.

Click the up arrow button a few more times while noticing the value of the area of the rectangles in the Report window after each doubling.

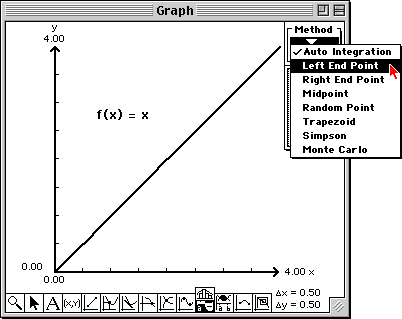
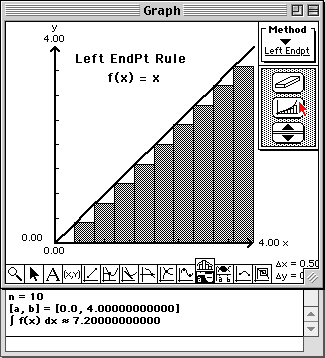
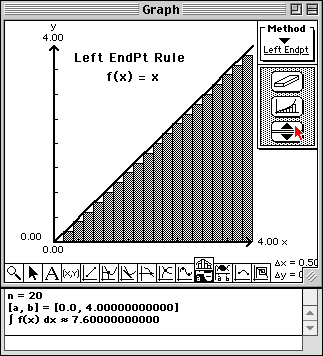
Notice that the values of the areas are converging to the area of the triangle and that the value of the area of the rectangles is a lower estimate to the area of the triangle.

Select Right End Point from the Method pop-up menu in the Graph window.
Enter "10" into the "n =" cell in the Domain & Range window. This resets the number of rectangles to 10.
Click the middle button (Draw button).
Click the up arrow button.

Click the up arrow button a few more times while noticing the value of the area of the rectangles in the Report window after each doubling.

Notice that the values of the areas are converging to the area of the triangle and that the value of the area of the rectangles is an upper estimate to the area of the triangle. The maximum number of rectangles that can be used in TEMATH is 4096.

We can conclude that area of the triangle is given by

Investigating unknown areas.

Plot g(x) = x^2+1 on 0x3 and 0y10. Note the change in the plotting domain and range.
If the Integration Tool's icon is not highlighted, click on the icon to select it.
Enter "10" into the "n =" cell in the Domain & Range window. This resets the number of rectangles to 10.

Follow the above process that was used for the triangular area and use upper and lower estimates to find the area under the curve between x = 0 and x = 3.

We can conclude that area under the curve between x = 0 and x = 3 is given by

Increasing the speed of convergence

We can conclude from the above activities that the area of the rectangles approach the area under the curve rather slowly. Can we speed up convergence? Let's try trapezoids instead of rectangles.

Select Trapezoid from the Method pop-up menu in the Graph window.
Enter "2" into the "n =" cell in the Domain & Range window. This resets the number of trapezoids to 2.
Click the middle button (Draw button).

Two shaded trapezoids are drawn and the value of their area is written into the Report window.
Click the up arrow button.

Click the up arrow button a few more times while noticing the value of the area of the trapezoids in the Report window after each doubling.

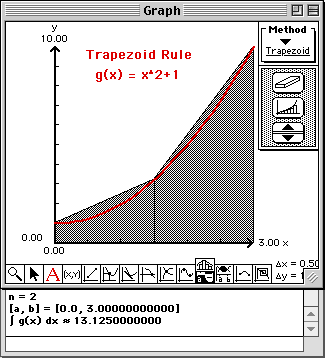
Notice that the values of the areas are converging much faster to the area under the curve.

Can we do better?

Plot h(x) = 6 + 10(x-3)(x-1) sin(3x) cos(x) on 0x3 and 0y25.

Follow the above process that was used for finding the area under the quadratic function g(x) = x^2+1. Use both rectangles and trapezoids and notice how fast the values of the areas of the rectangles (trapezoids) converge to the value of the area under the curve.

Select Simpson from the Method pop-up menu in the Graph window.
Enter "4" into the "n =" cell in the Domain & Range window.
Click the middle button (Draw button). The shaded areas under two parabolas are drawn and the value of their total area is written into the Report window.
Click the up arrow button.

Click the up arrow button a few more times while noticing the value of the area under the parabolas in the Report window after each doubling.

Notice that the values of the areas are converging much faster to the area under the curve than trapezoids.

Return to Topic Start

Return to Examples Menu