Most students know that if you are walking at a constant velocity, then
the distance that you walk is equal to your velocity times the amount of time that you walk, that
is, s = v t. Thus, if v = 4 ft/sec and t = 5 seconds, then s = 4(5) = 20 ft.
How far do you walk after 1 second? 2 seconds? 3 seconds? 4 seconds? t seconds?
To visualize the distance that you walk as a function of time,
- Click the Integration tool
 on
the Tool Palette in the Graph window.
on
the Tool Palette in the Graph window.
- Click in the upper rectangular region of the Integration tool's icon to view
the pop-up menu.

- Select "Dynamic" from the pop-up menu.

- Click the Go button.
Watch the area (total distance walked) under the plotted velocity function accumulate as a function of time.
Also, note that the value the total "area so far" under the curve is being plotted as the area is being
accumulated. Thus, the plotted line represents the distance that you walked as a function of time.
Note: You can click the Step button to move one time
increment at a time, you can click the Stop button to stop the Dynamic Integrator, or you
can click the Erase button to erase the drawn area and start a new plot. Also, you can
increase or decrease the speed of the Dynamic Integrator by selecting "Dynamic Plotting Speed..."
from the Options menu.
|
What is the equation of the line plotted by the Dynamic Integrator?
Let's extend the above concept of "distance walked as the total accumulated area under the velocity
curve" to velocity functions that are not constant. As an example, suppose that your velocity increases
linearly as you walk, that is, v = t + 2.
- Plot vl(t) on 0
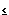 t
t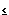 5 and
-5
5 and
-5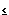 v
v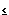 30.
30.
- Click the Go button.
Can you guess the type of function represented by the plotted distance curve?
What is the trapezoidal area under the velocity line between 0 and t?
Hint: use the formula for finding the area of a trapezoid.
Did you guess that s(t) = t^2/2 + 2t?
Negative Velocities
What happens if at some point in time your velocity is negative, that is, at some point
in time you are walking backwards. To find out, let's analyze the quadratic velocity function vq(t) = 2(t–1)(t–3.5) .
- Plot vq(t) on 0
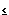 t
t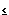 5 and
-5
5 and
-5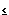 v
v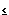 30.
30.
- Click the Go button.
Can you guess the type of function represented by the plotted "distance" curve?
Does the plotted "distance" curve represent the total distance walked?
If not, what does the curve plotted by the Dynamic Integrator represent?
What does the area "under" the velocity curve where the curve is below the t-axis represent?
How could you find the total distance walked?
Piecewise Velocity Function
- Plot vp(t) on 0
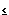 t
t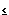 5 and
-5
5 and
-5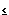 v
v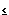 30.
30.
- Click the Go button.
Where is the distance function increasing at a constant rate?
Where is the distance function increasing the fastest?
Where is the distance function increasing the slowest?
Guessing the Form of the Distance Function (Antiderivatives)
- Plot vc(t) on 0
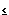 t
t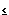 10 and
-5
10 and
-5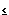 v
v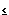 30. Note the change in the t plotting domain.
30. Note the change in the t plotting domain.
- Click the Go button.
Note that the curve plotted by the Dynamic Integrator does not represent the total
distance you walked in t secs, but, it represents your distance at time t from your starting point.
Can you guess the function that is represented by the curve plotted by the Dynamic Integrator?
- Select New Function from the Work menu.
- Enter the expression for your guessed function into the first cell of the
Work window. Press the Enter key.
- Select Overlay Plot from the Graph menu. Does your function match
the curve plotted by the Dynamic Integrator? If not, edit your function expression and try again.
Copyright 2000-2008 Adam O. Hausknecht and Robert E. Kowalczyk


![]()
![]()