Using the Fixed-Point Iteration Tool to Investigate "Orbits"

Caution: TEMATH's tools will write the values of computed results at the bottom of this Report window. This will cause you to constantly scroll between the computed results and the instructions for this activity. You may want to print a copy of the contents of the Report window before you begin this activity.

Fixed-point iteration is defined by the iteration process

x[n+1] = f(x[n]), n = 0, 1, 2, 3, ..., where the value of x[0] is given.

For example, if f(x) = 1.5x(1-x) and x0 = 0.6, then

x1 = 1.5(0.6)(1–0.6) = 0.36
x2 = 1.5(0.36)(1-0.36) = 0.3456
x3 = 1.5(0.3456)(1-0.3456) = 0.33924096
.
.
.

This sequence converges to the fixed point 0.333333333333.

You can use TEMATH's Fixed-Point Iteration tool to visualize this process.

Plot y1(x) on 0x1.
Click the Fixed-Point Iteration tool on the Tool Palette in the Graph window.
Click in the Graph window near x = 0.6 to enter the initial value x0 = 0.6. To enter this value more accurately, type 0.6 into the "x =" cell" in the Domain & Range window and press the Enter key.
Click the "Step" button to perform the next iteration.
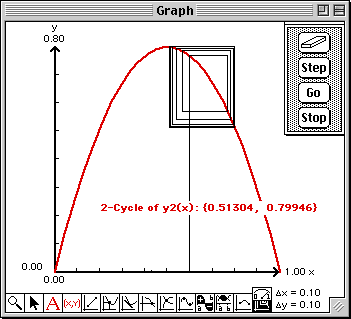
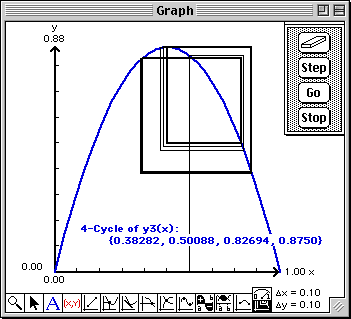
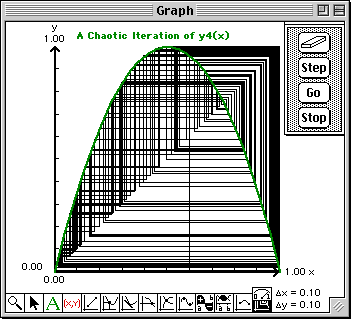
To view the calculated value of the next iterate, hold down the "option" key while you click the "Step" button. The value will be written into this Report window. You can also observe the value of the current iterate in the bottom cell of the Domain & Range window.
Click the "Step" button to perform the next iteration.
You can continue to click the "Step" button and perform one iteration at a time or you can click the "Go" button and iterations will be performed until they converge to a fixed point or until they reach the maximum number of iterations set by TEMATH. If the iterations converge to a fixed point, the value of the fixed point will be written into this Report window.
If you haven't done so already, click the "Go" button to find the fixed point at x = 0.333333333.

Iteration of y1(x)=1.5x(1-x) with x0 = 0.6

What else can happen in the fixed-point iteration process besides the sequence of iterates converging to a fixed point or diverging. To find out,

Plot y2(x) on 0x1.
Click in the Graph window near x = 0.6 to enter the initial value x0 = 0.6. To enter this value more accurately, type 0.6 into the "x =" cell" in the Domain & Range window and press the Enter key.
Click the "Go" button.

Note that the iterations end up cycling back and forth between 0.51304 and 0.79946.

Let's change the function from 3.2x(1-x) to 3.5x(1-x).

Plot y3(x) on 0x1.
Click in the Graph window near x = 0.6 to enter the initial value x0 = 0.6.
Click the "Go" button.

Note that this time, the iterations end up cycling back and forth between four values: 0.38282, 0.50088, 0.82694, and 0.8750.

As a last example, let's change the function to 4x(1-x).

Plot y4(x) on 0x1.
Click in the Graph window near x = 0.6 to enter the initial value x0 = 0.6.
Click the "Go" button.

Note that this time, the iterations have no pattern. The behavior of the iterations appears to be chaotic.

Return to Topic Start

Return to Examples Menu