Differential Equations

TEMATH has a set of numerical and qualitative tools that you can use to analyze the solution to a first or second order differential equation.

Caution: TEMATH's tools will write the values of computed results at the bottom of this Report window. This will cause you to constantly scroll between the computed results and the instructions for this activity. You may want to print a copy of the contents of the Report window before you begin this activity.

Logistic Growth

Suppose that a population can be modeled by the logistic equation

dy/dt = 0.4y(1 - y/3)

Use qualitative and numerical techniques to describe the population over time.

Select Diff Eq from the Graph menu.
This opens TEMATH's differential equation solver and makes available tools for analyzing differential equations.
Select New Differential Eqn - First Order from the Work menu.
Enter the expression 0.4y(1 - y/3) into the first cell in the Work window.

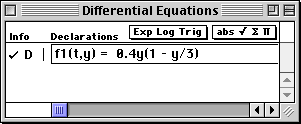
TEMATH assumes that the differential equation is written in the form

dy/dt = f(t, y).
Click the Axes button in the Graph window.
Axes will be drawn using the values in the Domain & Range window.
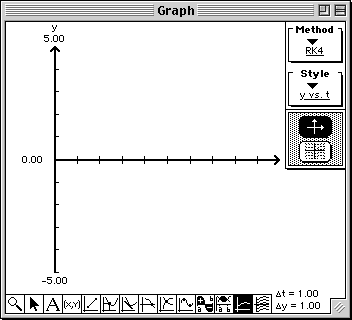
Click the Slope Field button.
The slope field will be drawn in the Graph window.

The Solution Curve tool icon

on the tool palette becomes highlighted when a differential equation is selected in the Work window and the axes have been plotted in the Graph window. This tool allows you to draw solution curves in the Graph window. If this tool is not highlighted, you must select it by clicking on it before you can draw a solution curve.

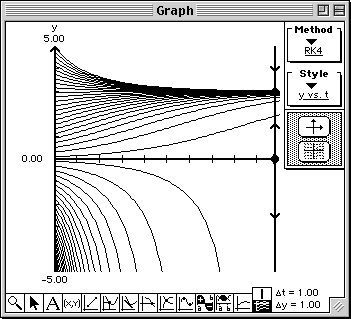
Position the cursor near the point (t, y) = (0, 5). Click the mouse button.
A solution curve to the differential equation will be drawn with initial value y(0) = 5. Also, note that the Phase line is drawn vertically on the right side of the Graph. The values of the equilibrium solutions (y = 0 and y = 3) are written into this Report window and circles are drawn on the Phase line denoting the equilibrium points. Note that the direction arrows on the Phase line indicate that y = 0 is a source and y = 3 is a sink.
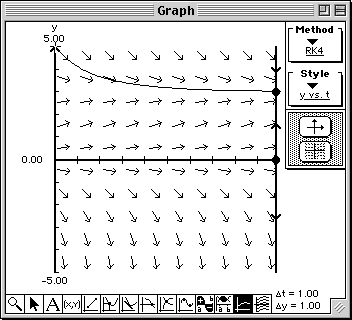
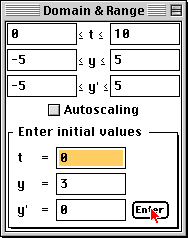
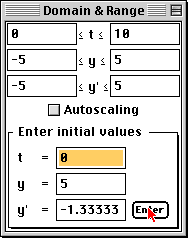
To enter the initial value more accurately, you can use the Domain & Range window by entering 0 into the "t =" cell, entering 5 into the "y =" cell, and clicking the Enter button or pressing the Enter key.
Draw solution curves for the following initial values: y(0) = 4, y(0) = 2, y(0) = 1, y(0) = 0.25, and y(0) = -0.25.

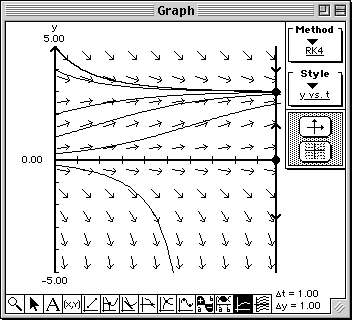
Describe the behavior of the solutions as t gets large.

To draw a Family of Solutions,

Click the Family of Solutions tool on the tool palette.
Position the cursor on the y-axis (that is, t = 0) and click the mouse button.
Fifty solution curves will be drawn in the Graph window.

Logistic Growth with Periodic Harvesting

Suppose that a population can be modeled by the logistic equation with periodic harvesting

dy/dt = 0.4y(1 - y/3) - 0.25 sin(t)

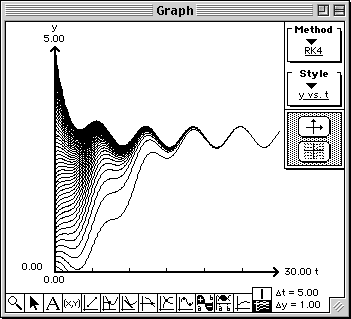
Use qualitative and numerical techniques to describe the population over time.

Select New Differential Eqn - First Order from the Work menu.
Enter the expression 0.4y(1 - y/3) - 0.25 sin(t) into the first cell in the Work window.
Click in the Domain & Range window to make it the active window. Enter the plotting domain 0 t30 and the plotting range 0y5.
Click the Axes button in the Graph window.
The Graph window will be cleared and axes will be drawn using the new values in the Domain & Range window.
If the Family of Solutions tool on the tool palette is not highlighted, click on it to select it.
Position the cursor on the y-axis (that is, t = 0) and click the mouse button.
Fifty solution curves will be drawn in the Graph window.

Describe the long term behavior of the solution curves.

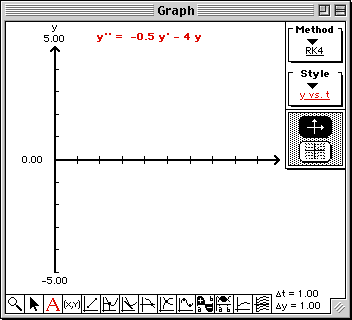
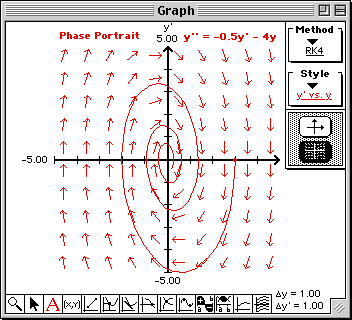
Damped Harmonic Oscillator

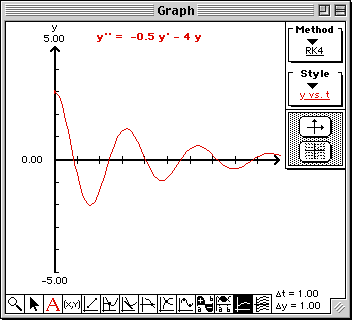
A damped harmonic oscillator is modeled by the following second order differential equation

y''(t) + 0.5 y'(t) + 4 y(t) = 0.

To enter this differential equation into TEMATH, we need to write it in the form

y''(t) = f(t, y, y') = -0.5 y'(t) - 4 y(t).

Use qualitative and numerical techniques to describe the harmonic oscillator over time.

Select New Differential Eqn - Second Order from the Work menu.
Enter the expression -0.5y' - 4y into the first cell in the Work window.
Click in the Domain & Range window to make it the active window.
Enter the plotting domain 0t10 and the plotting ranges -5 y 5 and -5y'5.
Click the Axes button in the Graph window.
The Graph window will be cleared and axes will be drawn using the values in the Domain & Range window.
If the Solution Curve tool on the tool palette is not highlighted, click on it to select it.

To draw an example solution curve, you need to enter some initial conditions.

Click in the Domain & Range window to make it the active window.
Enter the initial conditions y(0) = 3 and y'(0) = 0 by typing 0 into the "t =" cell, 3 into the "y =" cell, and 0 into the "y' =" cell.
Click the Enter button or press the Enter key.

The solution curve will be drawn in the Graph window.

A different view of the solution is given by examining its phase portrait in the phase plane.

Select "y' vs. y" from the Style pop-up menu in the Graph window.

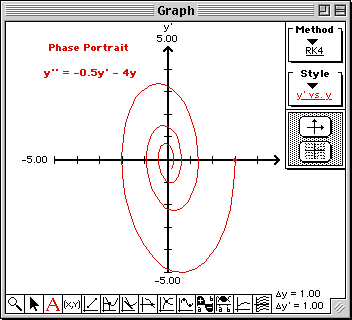
Additional information is given about the solutions to the differential equation by examining its direction field.

Click the Direction Field button to draw the direction field in the Graph window.

Return to Topic Start

Return to Examples Menu