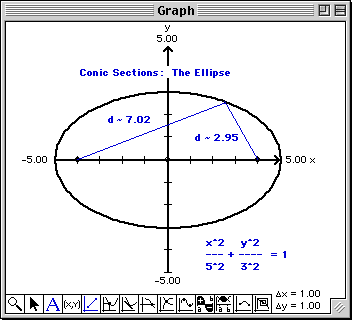
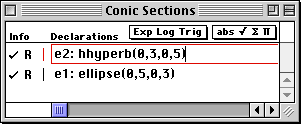
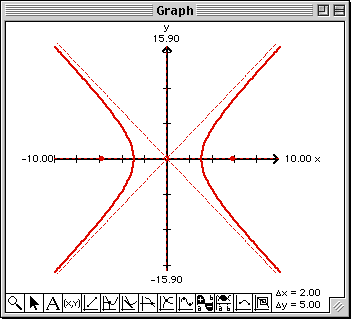
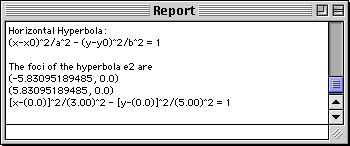
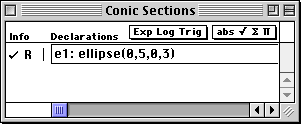
The ellipse template "e1: ellipse(x0,a,y0,b)" is written into the top cell of the Work window and the algebraic form of the ellipse "(x-x0)^2/a^2 + (y-y0)^2/b^2 = 1" is written at the bottom of this Report window.
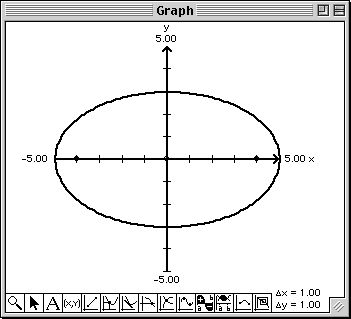
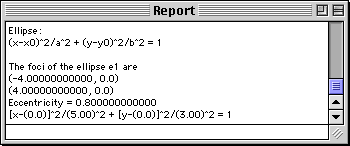
Note that solid circles are drawn at the locations of the foci and a circle is drawn at the center of the ellipse. Additionally, the coordinates of the foci and the eccentricity of the ellipse are written into this Report window. To control what conic annotations will be displayed with the plot, select Conic Annotations... from the Options menu.
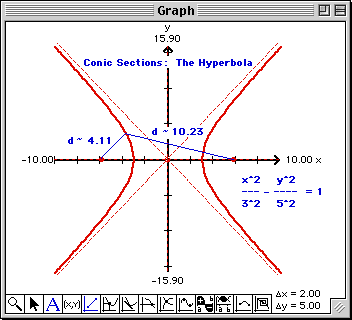
Draw a line from the left focus point F1 to any point P on the ellipse. Draw a second line from the point P to the right focus point F2. The lengths of the two line segments, |F1P| and |F2P|, are written into TEMATH's Report window.