Catenary - Modeling a Hanging Chain

Hyperbolic functions are usually studied in a first-year calculus course. Just about every calculus book has an example or problem that uses the hyperbolic cosine function to model the shape of a hanging cable (power line, chain). Physics gives us the following model:

y = (T/w) cosh(wx/T)

where T is the tension in the cable at its lowest point and w is the weight of the cable per unit length.

The shape of the curve of the hanging cable is called a catenary.

How accurate is this model? We performed the following experiment to find out.

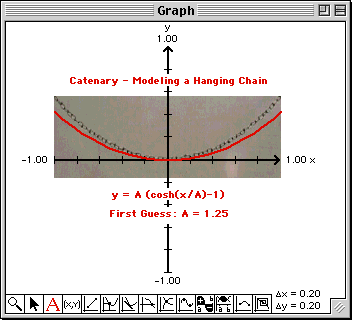
We had two of our students hold a chain in the front of the classroom. Using a digital camera, we took a picture of the hanging chain. (You can also hang the chain between two fixed supports). We downloaded the picture into our computer and used a picture viewing software package to display the picture. Using copy and paste, we copied the picture and pasted it on top of the axes plotted in TEMATH's Graph window. Using TEMATH's Selection tool

on the tool palette and the arrow keys on the keyboard, we repositioned the picture so that the lowest point on the hanging chain was placed at the origin. To see the entire chain picture,

Select Axes Style... from the Graph menu.
The Axes Style window will be displayed.
Enter 575 for the horizontal axis pixel length and 400 for the vertical axis pixel length.
Click the OK button.

Since the y-intercept of the model curve y = (T/w) cosh(wx/T) is equal to T/w, we need to shift the model down T/w units so that it passes through the origin (that is where we placed the "y-intercept" of the picture of the hanging chain). Thus, our model becomes

y = (T/w)(cosh(wx/T) - 1).

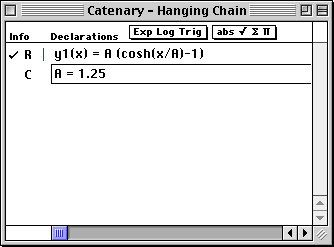
Finally, we replaced the quantity (T/w) with the single parameter A to get

y = A (cosh(x/A) - 1).

To determine how well this theoretical function models the hanging chain, we need to find the value of the parameter A. We used the "Estimate and Improve" method.

The Work window contains the initial estimate A = 1.25.

Select y1(x) in the Work window.
Select Plot from the Graph menu.

Note that the curve does not match the shape of the hanging chain very well. We need to improve our estimate of A.

Change the value of A in the Work window.
Select y1(x) in the Work window.
Select Plot from the Graph menu.

Continue to change (improve) the value of A until you find a perfect match between the curve of the model and the shape of the hanging chain.

Fit of a hanging chain

Catenary - Hanging Chain Work window

Return to Topic Start

Return to Examples Menu