The Trans-Alaska Pipeline starts in Prudhoe Bay in the High Arctic, crosses the Alaskan Arctic tundra,
and ends in Valdez on Prince Williams Sound. Oil must be heated so that it can easily flow through the pipeline. However,
the heat from the oil is transferred to the pipe and its supports. The engineers responsible for designing and building
the pipeline had to use insulated pads at the bottom of the pipe supports to keep the heat from the hot oil from melting
the permafrost (permanently frozen soil) beneath. If not, the pipe would eventually sink into the ground. In designing
the pads, the engineers needed to take into account the variation in air temperature throughout the year, that is, they
needed a mathematical model for air temperature. As an example, since the pipeline passes through Fairbanks, Alaska, the
engineers obtained the historical normal mean air temperature for Fairbanks for each day of the year.
General Sine Function
The general sine function can be written in the form
f(t) = a sin(2 /b (t-h)) + v
|
where a, b, h, and v are real numbers. a is the amplitude which is half the distance between
maximum and minimum values. b is the period which is the time needed for the function to execute one complete cycle.
h is the horizontal shift. v is the vertical shift.
Problem
Estimate the values of the parameters a, b, h, and v to find a sine function that fits the
Fairbanks temperature data.
This problem is based on an example from the textbook: Finney, Thomas, Demana, and Waits,
"Calculus A Graphing Approach", Addison-Wesley Publishing Co., 1993.
Instructions
- Read the Trans-Alaska Pipeline description.
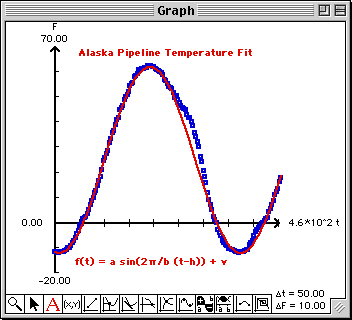
- Plot the data table Txy1[153,2].
- Click the Point tool
in
the Graph window and select (t, F) from its pop-up menu so that the coordinates of a point are displayed.
- Click a point at the minimum value of the plotted data and at the maximum value.
- Use the coordinates of the points to estimate the amplitude a.
- Use intuition to estimate the period b.
- Click a point at the translated origin of the sine curve and use the coordinates to estimate
the shift parameters h and v.
- Overlay the plot of f(t) = a sin(2
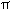/b (t-h)) + v
on top of the plotted data.
- How well does the sine curve fit the data?
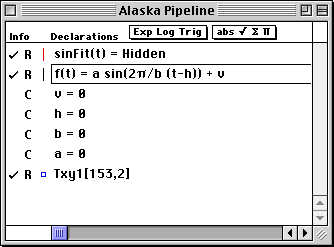
- The hidden function "sinFit(x) = Hidden" contains the expression for a sine fit
to the temperature data. To see the expression, select the hidden function in the Work window and then select
Show Hidden Function from the Options menu.
Copyright 2000-2008 Adam O. Hausknecht and Robert E. Kowalczyk